DeepONet: Operator Learning with Neural Networks¶
Learning Objectives:
- Understand the leap from function approximation to operator learning
- Master the Universal Approximation Theorem for Operators
- Learn the DeepONet architecture: Branch and Trunk networks
- Implement operator learning for the derivative operator
- Apply DeepONet to the 1D nonlinear Darcy problem
Slides:  ¶
¶
The Fundamental Question¶
We've learned how neural networks can approximate functions: $f: \mathbb{R}^d \rightarrow \mathbb{R}^m$.
But what if we want to learn mappings between infinite-dimensional function spaces?
Enter operators: mappings that take functions as input and produce functions as output.
$$\mathcal{G}: \mathcal{A} \rightarrow \mathcal{U}$$
where $\mathcal{A}$ and $\mathcal{U}$ are function spaces.
Examples of operators:
- Derivative operator: $\mathcal{G}u = \frac{du}{dx}$
- Integration operator: $\mathcal{G}f = \int_0^x f(t) dt$
- PDE solution operator: Given boundary conditions or source terms, map to the PDE solution.
The Challenge with Traditional Neural Networks¶
Standard neural networks learn point-wise mappings: $\mathbb{R}^n \rightarrow \mathbb{R}^m$. But operators map functions to functions. How do we represent infinite-dimensional functions with finite data?
Traditional approach limitations:
- Fixed discretization: Networks trained on specific grids can't generalize to different resolutions.
- Curse of dimensionality: High-dimensional function spaces are computationally intractable.
- No theoretical foundation: No guarantee that standard networks can approximate operators.
import numpy as np
import warnings
import torch
import torch.nn as nn
import torch.optim as optim
from tqdm import tqdm
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, TensorDataset
warnings.filterwarnings('ignore')
# Set style and random seeds
np.random.seed(42)
torch.manual_seed(42)
# Device selection
def get_device():
if torch.cuda.is_available():
return torch.device("cuda")
elif torch.backends.mps.is_available():
return torch.device("mps")
else:
return torch.device("cpu")
device = get_device()
print(f"Using device: {device}")
Using device: mps
From Scalars to Functions - The Conceptual Leap¶
Let's start with something familiar and build our intuition.
Traditional Function Approximation¶
We know neural networks can learn mappings like:
- Input: A number $x = 2.5$
- Output: A number $f(x) = x^2 = 6.25$
This is point-wise mapping: each input point maps to an output point.
Operator Learning: The Next Level¶
Now imagine:
- Input: An entire function $u(x) = \sin(x)$
- Output: Another entire function $\mathcal{G}[u](x) = \cos(x)$ (the derivative!)
This is function-to-function mapping: each input function maps to an output function.
Examples of operators we encounter in science:
- Derivative operator: $\mathcal{D}[u] = \frac{du}{dx}$
- Integration operator: $\mathcal{I}[f] = \int_0^x f(t) dt$
- PDE solution operator: Given source $f$, return solution $u$ of $\nabla^2 u = f$
def demonstrate_function_approximation():
"""Show traditional function approximation with clearer visualization"""
# Example: Learn f(x) = x² + sin(x)
x = np.linspace(-3, 3, 100)
y = x**2 + np.sin(x)
plt.figure(figsize=(15, 5))
# Plot 1: Traditional function plot
plt.subplot(1, 3, 1)
plt.plot(x, y, 'b-', linewidth=2, label='f(x) = x² + sin(x)')
plt.title('Traditional Function Approximation\nf: R → R')
plt.xlabel('Input x')
plt.ylabel('Output f(x)')
plt.grid(True, alpha=0.3)
plt.legend()
# Plot 2: Point-wise mapping visualization (improved)
plt.subplot(1, 3, 2)
# Show specific input-output pairs
sample_x = np.array([-1.0, 0.0, 1.0, 2.0])
sample_y = sample_x**2 + np.sin(sample_x)
# Create a clearer mapping visualization
input_positions = np.arange(len(sample_x))
output_positions = np.arange(len(sample_x)) + 0.5
# Plot input values
for i, (xi, yi) in enumerate(zip(sample_x, sample_y)):
# Input side
plt.scatter(0, input_positions[i], s=100, c='blue', zorder=5)
plt.text(-0.3, input_positions[i], f'x={xi:.1f}', ha='right', va='center')
# Output side
plt.scatter(2, input_positions[i], s=100, c='red', zorder=5)
plt.text(2.3, input_positions[i], f'f(x)={yi:.2f}', ha='left', va='center')
# Arrow showing mapping
plt.arrow(0.1, input_positions[i], 1.8, 0,
head_width=0.1, head_length=0.1, fc='gray', ec='gray', alpha=0.7)
plt.xlim(-0.5, 2.8)
plt.ylim(-0.5, len(sample_x) - 0.5)
plt.title('Point-wise Mapping\nScalar Input → Scalar Output')
plt.text(0, -0.8, 'Input Space R', ha='center', fontsize=12, fontweight='bold')
plt.text(2, -0.8, 'Output Space R', ha='center', fontsize=12, fontweight='bold')
plt.axis('off')
# Plot 3: Characteristics
plt.subplot(1, 3, 3)
plt.text(0.1, 0.9, 'Traditional Neural Networks:', fontsize=14, fontweight='bold',
transform=plt.gca().transAxes)
plt.text(0.1, 0.75, '• Input: Single numbers (scalars)', fontsize=12,
transform=plt.gca().transAxes)
plt.text(0.1, 0.65, '• Output: Single numbers (scalars)', fontsize=12,
transform=plt.gca().transAxes)
plt.text(0.1, 0.55, '• Learn: Point-wise mappings', fontsize=12,
transform=plt.gca().transAxes)
plt.text(0.1, 0.45, '• Architecture: Standard feedforward', fontsize=12,
transform=plt.gca().transAxes)
plt.text(0.1, 0.3, 'Examples:', fontsize=12, fontweight='bold',
transform=plt.gca().transAxes)
plt.text(0.1, 0.2, '• f(x) = x²', fontsize=12,
transform=plt.gca().transAxes, style='italic')
plt.text(0.1, 0.1, '• Classification problems', fontsize=12,
transform=plt.gca().transAxes, style='italic')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.axis('off')
plt.title('Characteristics')
plt.tight_layout()
plt.show()
print("Traditional Function Approximation:")
print("• Takes individual points as input")
print("• Produces individual points as output")
print("• Neural network learns: x → f(x)")
print("• This is what we're familiar with!")
demonstrate_function_approximation()
Traditional Function Approximation: • Takes individual points as input • Produces individual points as output • Neural network learns: x → f(x) • This is what we're familiar with!
Operator Learning¶
def demonstrate_operator_concept():
"""Demonstrate the concept of operators"""
x = np.linspace(-2, 2, 100)
# Three different input functions
u1 = x**2
u2 = np.sin(2*x)
u3 = np.exp(-x**2)
# The derivative operator D applied to each
du1_dx = 2*x
du2_dx = 2*np.cos(2*x)
du3_dx = -2*x*np.exp(-x**2)
plt.figure(figsize=(15, 10))
# Show operator concept
for i, (u, du_dx, title) in enumerate([(u1, du1_dx, 'u(x) = x²'),
(u2, du2_dx, 'u(x) = sin(2x)'),
(u3, du3_dx, 'u(x) = e^(-x²)')]):
plt.subplot(3, 3, 3*i + 1)
plt.plot(x, u, 'b-', linewidth=2)
plt.title(f'Input Function\n{title}')
plt.xlabel('x')
plt.ylabel('u(x)')
plt.grid(True, alpha=0.3)
plt.subplot(3, 3, 3*i + 2)
plt.arrow(0.3, 0.5, 0.4, 0, head_width=0.1, head_length=0.05, fc='green', ec='green', linewidth=3)
plt.text(0.5, 0.7, 'Derivative\nOperator $\mathcal{D}$', ha='center', fontsize=12, fontweight='bold')
plt.text(0.5, 0.3, '$\mathcal{D}$[u] = du/dx', ha='center', fontsize=10, style='italic')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.axis('off')
plt.title('Apply Operator')
plt.subplot(3, 3, 3*i + 3)
plt.plot(x, du_dx, 'r-', linewidth=2)
derivative_titles = ['2x', '2cos(2x)', '-2xe^(-x²)']
plt.title(f'Output Function\ndu/dx = {derivative_titles[i]}')
plt.xlabel('x')
plt.ylabel('du/dx')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Key Insight: An operator takes a FUNCTION as input and produces a FUNCTION as output!")
print("This is fundamentally different from traditional function approximation.")
demonstrate_operator_concept()
Key Insight: An operator takes a FUNCTION as input and produces a FUNCTION as output! This is fundamentally different from traditional function approximation.
The Universal Approximation Theorem for Operators¶
The Breakthrough Theorem¶
Just as the Universal Approximation Theorem tells us neural networks can approximate functions, there's a remarkable extension:
Theorem (Chen & Chen, 1995): Neural networks can approximate operators that map functions to functions!
Mathematical Statement: For any continuous operator $\mathcal{G}: V \subset C(K_1) \rightarrow C(K_2)$ and $\epsilon > 0$, there exist constants such that:
$$\left|\mathcal{G}(u)(y) - \sum_{k=1}^p \underbrace{\sum_{i=1}^n c_i^k \sigma\left(\sum_{j=1}^m \xi_{ij}^k u(x_j) + \theta_i^k\right)}_{\text{Branch Network}} \underbrace{\sigma(w_k \cdot y + \zeta_k)}_{\text{Trunk Network}}\right| < \epsilon$$
Decoding the Theorem¶
This looks complex, but the insight is beautiful:
- Branch Network: Processes function $u$ sampled at sensor points $\{x_j\}$
- Trunk Network: Processes output coordinates $y$
- Combination: Multiply branch and trunk outputs, then sum
Key insight: Any operator can be written as: $$\mathcal{G}(u)(y) \approx \sum_{k=1}^p b_k(u) \cdot t_k(y)$$
where $b_k$ depends only on the input function and $t_k$ depends only on the output location!
Visualizing the Operator UAT Structure¶
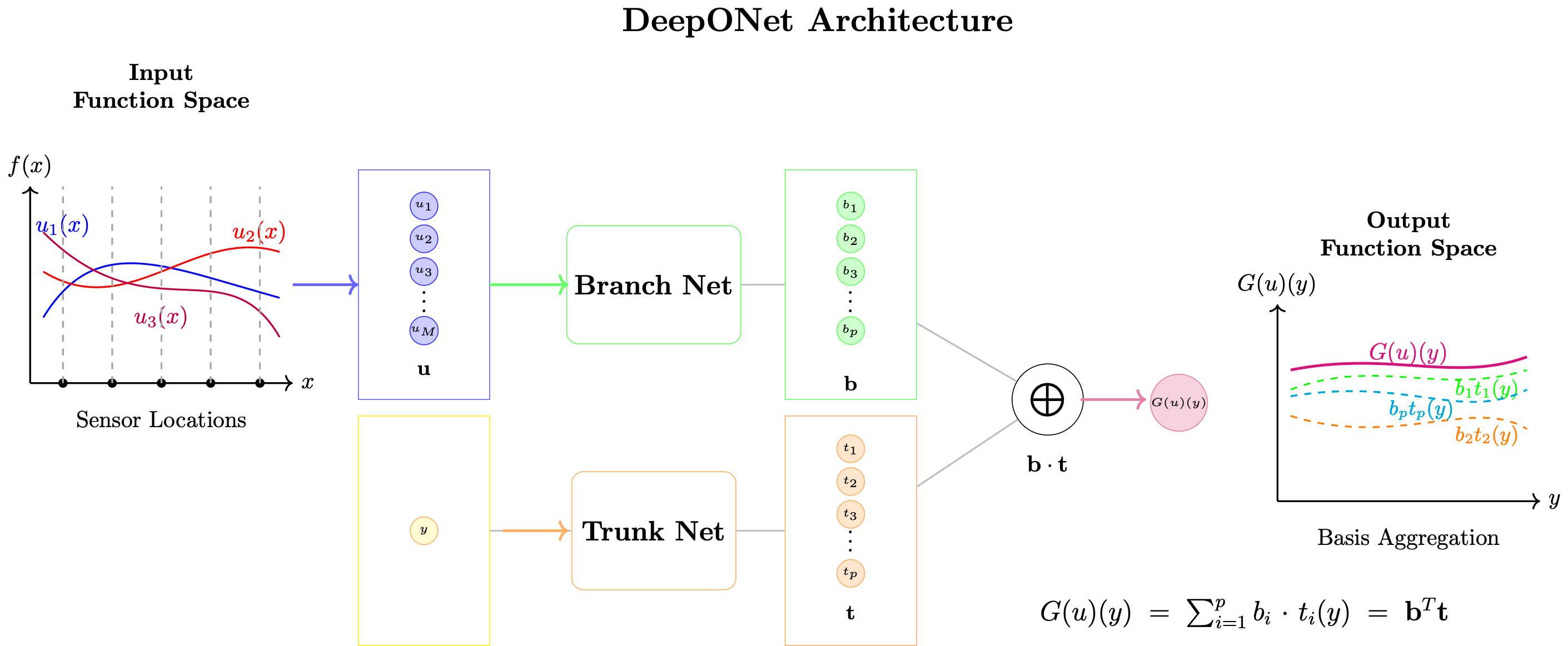
DeepONet Architecture¶
DeepONet (Deep Operator Network) is the practical implementation of the Operator Universal Approximation Theorem.
Core Architecture¶
$$\mathcal{G}_\theta(u)(y) = \sum_{k=1}^p b_k(u) \cdot t_k(y) + b_0$$
where:
- Branch network: $b_k(u) = \mathcal{B}_k([u(x_1), u(x_2), \ldots, u(x_m)])$
- Trunk network: $t_k(y) = \mathcal{T}_k(y)$
- $p$: Number of basis functions (typically 50-200)
- $b_0$: Bias term
Training Data Structure¶
Input-output pairs: $(u^{(i)}, y^{(j)}, \mathcal{G}(u^{(i)})(y^{(j)}))$
- $N$ input functions: $\{u^{(i)}\}_{i=1}^N$
- Each function sampled at $m$ sensors: $\{u^{(i)}(x_j)\}_{j=1}^m$
- Corresponding outputs at query points: $\{\mathcal{G}(u^{(i)})(y_k)\}$
Loss Function¶
$$\mathcal{L}(\theta) = \frac{1}{N \cdot P} \sum_{i=1}^N \sum_{k=1}^P \left|\mathcal{G}_\theta(u^{(i)})(y_k) - \mathcal{G}(u^{(i)})(y_k)\right|^2$$
Key Advantages¶
- Resolution independence: Train on one grid, evaluate on any grid
- Fast evaluation: Once trained, instant prediction (no iterative solving)
- Generalization: Works for new functions not seen during training
- Physical consistency: Learns the underlying operator
Concrete Example - The Derivative Operator¶
Perfect starting point: Learn the derivative operator $\mathcal{D}[u] = \frac{du}{dx}$
Why this example:
- Simple and intuitive
- Exact analytical solution for verification
- Shows how DeepONet learns basis decompositions
- Bridges function approximation → operator learning
Problem Setup¶
Input functions: Cubic polynomials $u(x) = ax^3 + bx^2 + cx + d$
Target operator: $\mathcal{D}[u](x) = \frac{du}{dx} = 3ax^2 + 2bx + c$
Key insight: The derivative of a cubic is always quadratic, so it can be written as: $$\frac{du}{dx} = w_1 \cdot 1 + w_2 \cdot x + w_3 \cdot x^2$$
where $w_1 = c$, $w_2 = 2b$, $w_3 = 3a$.
The DeepONet challenge: Can it learn this mapping automatically?
Data Generation for DeepONet¶
Key Concept: We're learning the derivative operator $D[u] = du/dx$
For cubic polynomials $u(x) = ax^3 + bx^2 + cx + d$
The derivative is $u^\prime(x) = 3ax^2 + 2bx + c$
# ========================= CELL 1: Data Generation =========================
def generate_polynomial_data(num_functions=2000, num_points=100, x_range=(-2, 2)):
"""Generate cubic polynomial functions and their derivatives"""
np.random.seed(42)
# Generate random coefficients for cubic polynomials: ax^3 + bx^2 + cx + d
coeffs = np.random.randn(num_functions, 4) * 0.5
# Generate spatial points
x = np.linspace(x_range[0], x_range[1], num_points)
# Initialize arrays
functions = np.zeros((num_functions, num_points))
derivatives = np.zeros((num_functions, num_points))
for i in range(num_functions):
a, b, c, d = coeffs[i]
# f(x) = ax^3 + bx^2 + cx + d
functions[i] = a * x**3 + b * x**2 + c * x + d
# f'(x) = 3ax^2 + 2bx + c
derivatives[i] = 3 * a * x**2 + 2 * b * x + c
return coeffs, x, functions, derivatives
print("=== POLYNOMIAL DATA GENERATION ===")
coeffs, x, functions, derivatives = generate_polynomial_data(num_functions=2000, num_points=100)
print(f"Generated {len(coeffs)} polynomial functions")
print(f"Coefficient shape: {coeffs.shape} (a, b, c, d for ax³+bx²+cx+d)")
print(f"Spatial domain: x ∈ [{x[0]:.1f}, {x[-1]:.1f}] with {len(x)} points")
print(f"Functions shape: {functions.shape}")
print(f"Derivatives shape: {derivatives.shape}")
# Visualize sample polynomials and their derivatives
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
for i in range(6):
ax = axes[i//3, i%3]
# Plot function and derivative
ax.plot(x, functions[i], 'b-', linewidth=2, label=f'f(x)', alpha=0.8)
ax.plot(x, derivatives[i], 'r-', linewidth=2, label=f"f'(x)", alpha=0.8)
# Show coefficients
a, b, c, d = coeffs[i]
ax.set_title(f'Sample {i+1}: [{a:.2f}, {b:.2f}, {c:.2f}, {d:.2f}]')
ax.grid(True, alpha=0.3)
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('Value')
plt.tight_layout()
plt.savefig('polynomial_samples.png', dpi=150)
plt.show()
# Print some mathematical relationships
print("\nMathematical relationships:")
print("f(x) = ax³ + bx² + cx + d")
print("f'(x) = 3ax² + 2bx + c")
print("Goal: Learn operator mapping [a,b,c,d] → f'(x)")
=== POLYNOMIAL DATA GENERATION === Generated 2000 polynomial functions Coefficient shape: (2000, 4) (a, b, c, d for ax³+bx²+cx+d) Spatial domain: x ∈ [-2.0, 2.0] with 100 points Functions shape: (2000, 100) Derivatives shape: (2000, 100)
Mathematical relationships: f(x) = ax³ + bx² + cx + d f'(x) = 3ax² + 2bx + c Goal: Learn operator mapping [a,b,c,d] → f'(x)
DeepONet Implementation¶
class DeepONet(nn.Module):
def __init__(self, branch_input_dim, trunk_input_dim, hidden_dim=32, num_basis=3):
super(DeepONet, self).__init__()
self.num_basis = num_basis
self.hidden_dim = hidden_dim
# Branch network - processes function coefficients
self.branch_net = nn.Sequential(
nn.Linear(branch_input_dim, hidden_dim),
nn.Tanh(),
nn.Linear(hidden_dim, num_basis)
)
# Trunk network - processes spatial coordinates
self.trunk_net = nn.Sequential(
nn.Linear(trunk_input_dim, hidden_dim),
nn.Tanh(),
nn.Linear(hidden_dim, num_basis)
)
# Bias term
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, branch_input, trunk_input):
# Branch network output
branch_out = self.branch_net(branch_input) # [batch_size, num_basis]
# Trunk network output - handle batch dimension
if trunk_input.dim() == 3: # [batch_size, num_points, 1]
batch_size, num_points, _ = trunk_input.shape
trunk_input_flat = trunk_input.view(-1, 1) # [batch_size * num_points, 1]
trunk_out = self.trunk_net(trunk_input_flat) # [batch_size * num_points, num_basis]
trunk_out = trunk_out.view(batch_size, num_points, self.num_basis) # [batch_size, num_points, num_basis]
else: # [num_points, 1] - single evaluation
trunk_out = self.trunk_net(trunk_input) # [num_points, num_basis]
trunk_out = trunk_out.unsqueeze(0) # [1, num_points, num_basis]
# Compute inner product
output = torch.einsum('bi,bpi->bp', branch_out, trunk_out)
return output + self.bias
print("\n=== DEEPONET ARCHITECTURE ===")
model = DeepONet(branch_input_dim=4, trunk_input_dim=1, hidden_dim=32, num_basis=3)
model = model.to(device)
total_params = sum(p.numel() for p in model.parameters())
trainable_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"DeepONet Architecture:")
print(f"- Branch input: 4 (polynomial coefficients [a,b,c,d])")
print(f"- Trunk input: 1 (spatial coordinate x)")
print(f"- Hidden dimension: {model.hidden_dim}")
print(f"- Number of basis functions: {model.num_basis}")
print(f"- Total parameters: {total_params:,}")
print(f"- Trainable parameters: {trainable_params:,}")
=== DEEPONET ARCHITECTURE === DeepONet Architecture: - Branch input: 4 (polynomial coefficients [a,b,c,d]) - Trunk input: 1 (spatial coordinate x) - Hidden dimension: 32 - Number of basis functions: 3 - Total parameters: 423 - Trainable parameters: 423
Training¶
def setup_data_loaders(coeffs, x, derivatives, batch_size=128):
"""Setup train/val/test data loaders"""
# Split data
train_size = int(0.8 * len(coeffs))
val_size = int(0.1 * len(coeffs))
train_coeffs = coeffs[:train_size]
train_derivatives = derivatives[:train_size]
val_coeffs = coeffs[train_size:train_size+val_size]
val_derivatives = derivatives[train_size:train_size+val_size]
test_coeffs = coeffs[train_size+val_size:]
test_derivatives = derivatives[train_size+val_size:]
# Convert to tensors
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(1)
# Create datasets - expand x_tensor for each function
train_x = x_tensor.unsqueeze(0).repeat(len(train_coeffs), 1, 1)
val_x = x_tensor.unsqueeze(0).repeat(len(val_coeffs), 1, 1)
train_dataset = TensorDataset(
torch.tensor(train_coeffs, dtype=torch.float32),
train_x,
torch.tensor(train_derivatives, dtype=torch.float32)
)
val_dataset = TensorDataset(
torch.tensor(val_coeffs, dtype=torch.float32),
val_x,
torch.tensor(val_derivatives, dtype=torch.float32)
)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
return train_loader, val_loader, (test_coeffs, test_derivatives)
def train_deeponet(model, train_loader, val_loader, num_epochs=500, lr=0.01):
"""Train the DeepONet model"""
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=1e-4)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, patience=50, factor=0.5)
criterion = nn.MSELoss()
train_losses = []
val_losses = []
best_val_loss = float('inf')
patience = 100
patience_counter = 0
# Progress bar
pbar = tqdm(range(num_epochs), desc="Training DeepONet")
for epoch in pbar:
# Training
model.train()
train_loss = 0.0
for batch_coeffs, batch_x, batch_derivatives in train_loader:
batch_coeffs = batch_coeffs.to(device)
batch_x = batch_x.to(device)
batch_derivatives = batch_derivatives.to(device)
optimizer.zero_grad()
output = model(batch_coeffs, batch_x)
loss = criterion(output, batch_derivatives)
loss.backward()
optimizer.step()
train_loss += loss.item()
# Validation
model.eval()
val_loss = 0.0
with torch.no_grad():
for batch_coeffs, batch_x, batch_derivatives in val_loader:
batch_coeffs = batch_coeffs.to(device)
batch_x = batch_x.to(device)
batch_derivatives = batch_derivatives.to(device)
output = model(batch_coeffs, batch_x)
loss = criterion(output, batch_derivatives)
val_loss += loss.item()
avg_train_loss = train_loss / len(train_loader)
avg_val_loss = val_loss / len(val_loader)
train_losses.append(avg_train_loss)
val_losses.append(avg_val_loss)
scheduler.step(avg_val_loss)
# Update progress bar
pbar.set_postfix({
'Train': f'{avg_train_loss:.6f}',
'Val': f'{avg_val_loss:.6f}',
'LR': f'{optimizer.param_groups[0]["lr"]:.6f}'
})
# Early stopping
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
patience_counter = 0
else:
patience_counter += 1
if patience_counter >= patience:
print(f'\\nEarly stopping at epoch {epoch}')
break
pbar.close()
return train_losses, val_losses
print("\n=== TRAINING ===")
train_loader, val_loader, test_data = setup_data_loaders(coeffs, x, derivatives, batch_size=128)
print(f"Data splits:")
print(f"- Training batches: {len(train_loader)} (batch size: 128)")
print(f"- Validation batches: {len(val_loader)}")
print(f"- Test samples: {len(test_data[0])}")
print("\\nStarting training...")
train_losses, val_losses = train_deeponet(model, train_loader, val_loader, num_epochs=500, lr=0.01)
# Plot training curves
plt.figure(figsize=(10, 6))
plt.plot(train_losses, label='Training Loss', alpha=0.8)
plt.plot(val_losses, label='Validation Loss', alpha=0.8)
plt.xlabel('Epoch')
plt.ylabel('MSE Loss')
plt.title('Training History')
plt.legend()
plt.grid(True, alpha=0.3)
plt.yscale('log')
plt.savefig('training_curves.png', dpi=150)
plt.show()
print(f"Training completed!")
print(f"Final training loss: {train_losses[-1]:.6f}")
print(f"Final validation loss: {val_losses[-1]:.6f}")
=== TRAINING === Data splits: - Training batches: 13 (batch size: 128) - Validation batches: 2 - Test samples: 200 \nStarting training...
Training DeepONet: 100%|██████████| 500/500 [00:29<00:00, 16.81it/s, Train=0.000439, Val=0.000770, LR=0.002500]
Training completed! Final training loss: 0.000439 Final validation loss: 0.000770
Evaluation of model¶
def evaluate_predictions(model, test_data, x):
"""Evaluate model predictions and create visualizations"""
test_coeffs, test_derivatives = test_data
model.eval()
# Compute test errors
test_errors = []
predictions = []
with torch.no_grad():
for i in range(len(test_coeffs)):
coeffs_tensor = torch.tensor(test_coeffs[i:i+1], dtype=torch.float32).to(device)
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(1).to(device)
predicted = model(coeffs_tensor, x_tensor).cpu().numpy().flatten()
true_derivative = test_derivatives[i]
mse = np.mean((predicted - true_derivative)**2)
test_errors.append(mse)
predictions.append(predicted)
avg_test_mse = np.mean(test_errors)
print(f"Average Test MSE: {avg_test_mse:.6f}")
print(f"Test MSE std: {np.std(test_errors):.6f}")
return predictions, test_errors
print("\\n=== PREDICTION & EVALUATION ===")
predictions, test_errors = evaluate_predictions(model, test_data, x)
test_coeffs, test_derivatives = test_data
# Plot prediction results
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
# Plot sample predictions
for i in range(6):
ax = axes[i//3, i%3]
ax.plot(x, test_derivatives[i], 'b-', linewidth=2, label='True f\'(x)', alpha=0.8)
ax.plot(x, predictions[i], 'r--', linewidth=2, label='Predicted f\'(x)', alpha=0.8)
# Show coefficients and error
coeffs_str = ', '.join([f'{c:.2f}' for c in test_coeffs[i]])
error = test_errors[i]
ax.set_title(f'Test {i+1}: [{coeffs_str}]\\nMSE: {error:.6f}')
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_xlabel('x')
ax.set_ylabel("f'(x)")
plt.tight_layout()
plt.savefig('prediction_results.png', dpi=150)
plt.show()
\n=== PREDICTION & EVALUATION === Average Test MSE: 0.000778 Test MSE std: 0.003893
Understanding What DeepONet Learned¶
Critical question: Did DeepONet truly learn the derivative operator, or just memorize patterns?
Let's test it on completely new types of functions it has never seen!
def extract_basis_equations(model, x_range=(-2, 2), num_points=1000):
"""Extract basis functions as polynomial equations by fitting"""
model.eval()
# Generate fine-grained x values for fitting
x_fine = np.linspace(x_range[0], x_range[1], num_points)
x_tensor = torch.tensor(x_fine, dtype=torch.float32).unsqueeze(1).to(device)
with torch.no_grad():
# Get trunk network outputs (basis functions)
basis_outputs = model.trunk_net(x_tensor).cpu().numpy() # [num_points, num_basis]
# Fit polynomials to each basis function
basis_equations = []
for i in range(model.num_basis):
y_basis = basis_outputs[:, i]
# Try different polynomial degrees and pick the best fit
best_coeffs = None
best_degree = 0
best_r2 = -np.inf
for degree in range(1, 5): # Try degrees 1-4
try:
coeffs = np.polyfit(x_fine, y_basis, degree)
y_pred = np.polyval(coeffs, x_fine)
# Calculate R² score
ss_res = np.sum((y_basis - y_pred) ** 2)
ss_tot = np.sum((y_basis - np.mean(y_basis)) ** 2)
r2 = 1 - (ss_res / ss_tot) if ss_tot != 0 else 0
if r2 > best_r2:
best_r2 = r2
best_coeffs = coeffs
best_degree = degree
except:
continue
# Format equation string
equation = format_polynomial_equation(best_coeffs, best_degree)
basis_equations.append({
'coefficients': best_coeffs,
'degree': best_degree,
'equation': equation,
'r2_score': best_r2,
'function_values': y_basis,
'x_values': x_fine
})
return basis_equations
def format_polynomial_equation(coeffs, degree):
"""Format polynomial coefficients as readable equation"""
if coeffs is None:
return "Unable to fit"
terms = []
for i, coeff in enumerate(coeffs):
power = degree - i
if abs(coeff) < 1e-6: # Skip negligible terms
continue
# Format coefficient
if len(terms) == 0: # First term
coeff_str = f"{coeff:.4f}"
else: # Subsequent terms
coeff_str = f"{coeff:+.4f}"
# Format power
if power == 0:
term = coeff_str
elif power == 1:
if abs(coeff - 1) < 1e-6:
term = "x" if len(terms) == 0 else "+x"
elif abs(coeff + 1) < 1e-6:
term = "-x"
else:
term = f"{coeff_str}x"
else:
if abs(coeff - 1) < 1e-6:
term = f"x^{power}" if len(terms) == 0 else f"+x^{power}"
elif abs(coeff + 1) < 1e-6:
term = f"-x^{power}"
else:
term = f"{coeff_str}x^{power}"
terms.append(term)
return " ".join(terms) if terms else "0"
def analyze_branch_behavior(model):
"""Analyze how branch network maps different polynomial types"""
model.eval()
# Test specific polynomial types
sample_coeffs = np.array([
[1, 0, 0, 0], # Pure cubic: ax³ → 3ax²
[0, 1, 0, 0], # Pure quadratic: bx² → 2bx
[0, 0, 1, 0], # Pure linear: cx → c
[0, 0, 0, 1] # Pure constant: d → 0
])
coeffs_labels = ['ax³→3ax²', 'bx²→2bx', 'cx→c', 'd→0']
print("Branch Network Analysis:")
print("Input polynomial term → Basis function weights")
with torch.no_grad():
for coeffs, label in zip(sample_coeffs, coeffs_labels):
coeffs_tensor = torch.tensor(coeffs.reshape(1, -1), dtype=torch.float32).to(device)
branch_out = model.branch_net(coeffs_tensor).detach().cpu().numpy().flatten()
weights_str = ', '.join([f'{w:.4f}' for w in branch_out])
print(f" {label}: [{weights_str}]")
return sample_coeffs, coeffs_labels
print("\\n=== BASIS FUNCTION ANALYSIS ===")
# Extract basis functions
print("Extracting learned basis functions...")
basis_equations = extract_basis_equations(model, x_range=(-2, 2))
# Visualize basis functions
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# Plot 1: Basis functions
model.eval()
with torch.no_grad():
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(1).to(device)
trunk_features = model.trunk_net(x_tensor).cpu().numpy()
colors = ['red', 'blue', 'green']
for i in range(model.num_basis):
axes[0,0].plot(x, trunk_features[:, i], linewidth=2,
label=f'φ_{i+1}(x)', color=colors[i])
axes[0,0].set_xlabel('x')
axes[0,0].set_ylabel('Basis Function Value')
axes[0,0].set_title('Learned Basis Functions φᵢ(x)')
axes[0,0].legend()
axes[0,0].grid(True, alpha=0.3)
# Plot 2: Branch network behavior
sample_coeffs, coeffs_labels = analyze_branch_behavior(model)
colors = ['red', 'blue', 'green', 'purple']
x_pos = np.arange(model.num_basis)
width = 0.2
for i, (coeffs, label) in enumerate(zip(sample_coeffs, coeffs_labels)):
coeffs_tensor = torch.tensor(coeffs.reshape(1, -1), dtype=torch.float32).to(device)
branch_out = model.branch_net(coeffs_tensor).detach().cpu().numpy().flatten()
axes[0,1].bar(x_pos + i*width, branch_out, width, alpha=0.7,
label=label, color=colors[i])
axes[0,1].set_xlabel('Basis Function Index')
axes[0,1].set_ylabel('Branch Weight')
axes[0,1].set_title('Branch Network: Polynomial Terms → Weights')
axes[0,1].set_xticks(x_pos + 1.5*width)
axes[0,1].set_xticklabels([f'φ_{i+1}' for i in range(model.num_basis)])
axes[0,1].legend()
axes[0,1].grid(True, alpha=0.3)
# Plot 3-4: Individual basis functions with fitted equations
for i in range(min(2, model.num_basis)):
ax = axes[1, i]
basis_info = basis_equations[i]
ax.plot(x, trunk_features[:, i], 'b-', linewidth=2, label='Learned φ(x)')
# Plot fitted polynomial
if basis_info['coefficients'] is not None:
x_fine = np.linspace(x[0], x[-1], 200)
y_fit = np.polyval(basis_info['coefficients'], x_fine)
ax.plot(x_fine, y_fit, 'r--', linewidth=2, label='Fitted polynomial')
ax.set_title(f'φ_{i+1}(x) = {basis_info["equation"]}\\nR² = {basis_info["r2_score"]:.4f}')
ax.set_xlabel('x')
ax.set_ylabel('φ(x)')
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('basis_analysis.png', dpi=150)
plt.show()
# Print mathematical formulation
print("\\n" + "="*60)
print("DEEPONET MATHEMATICAL DECOMPOSITION")
print("="*60)
print("Original problem: Learn operator T: [a,b,c,d] → f'(x)")
print("where f(x) = ax³ + bx² + cx + d")
print("and f'(x) = 3ax² + 2bx + c")
print()
print("DeepONet solution: f'(x) ≈ Σᵢ₌₁³ wᵢ(a,b,c,d) × φᵢ(x) + bias")
print()
print("Learned basis functions:")
for i, basis_info in enumerate(basis_equations):
print(f" φ_{i+1}(x) = {basis_info['equation']} (R² = {basis_info['r2_score']:.4f})")
\n=== BASIS FUNCTION ANALYSIS === Extracting learned basis functions... Branch Network Analysis: Input polynomial term → Basis function weights ax³→3ax²: [2.9438, -2.1361, 3.2953] bx²→2bx: [0.3271, 1.0190, 0.4438] cx→c: [-0.4119, -0.1281, 0.4185] d→0: [0.0199, 0.0062, -0.0214]
\n============================================================ DEEPONET MATHEMATICAL DECOMPOSITION ============================================================ Original problem: Learn operator T: [a,b,c,d] → f'(x) where f(x) = ax³ + bx² + cx + d and f'(x) = 3ax² + 2bx + c DeepONet solution: f'(x) ≈ Σᵢ₌₁³ wᵢ(a,b,c,d) × φᵢ(x) + bias Learned basis functions: φ_1(x) = -0.0008x^4 -0.0008x^3 +0.4409x^2 +0.2854x -1.2440 (R² = 1.0000) φ_2(x) = -0.0012x^4 -0.0005x^3 -0.2807x^2 +1.5516x -0.0966 (R² = 1.0000) φ_3(x) = -0.0012x^4 +0.0005x^3 +0.3411x^2 +0.7492x +1.0264 (R² = 1.0000)
The 1D Nonlinear Darcy Problem¶
Now for something more challenging: A real PDE with nonlinear physics!
Problem Formulation¶
The 1D nonlinear Darcy equation models groundwater flow with solution-dependent permeability:
$$\frac{d}{dx}\left(-\kappa(u(x))\frac{du}{dx}\right) = f(x), \quad x \in [0,1]$$
where:
u(x)is the solution field (e.g., pressure or hydraulic head).- The $\kappa(u)$: is non-linear solution-dependent permeability is
κ(u(x)) = 0.2 + u^2(x). - The input term
f(x)is a Gaussian random field defined asf(x) ~ GP(0, k(x, x'))such thatk(x, x') = σ^2 exp(-||x - x'||^2 / (2ℓ_x^2)), whereℓ_x = 0.04andσ^2 = 1.0. - Homogeneous Dirichlet boundary conditions
u(0) = 0andu(1) = 0are considered at the domain boundaries.
The Operator Learning Challenge¶
Goal: Learn the solution operator $\mathcal{G}$ such that: $$\mathcal{G}[f] = u$$
where $u$ is the solution to the nonlinear Darcy equation for source $f$.
Key insight: This is much harder than the derivative operator because:
- Nonlinear PDE: No analytical solution
- Random sources: Infinite variety of input functions
- Complex physics: Solution depends on entire source profile
Why This Matters¶
Traditional approach: For each new source $f$, solve the PDE numerically (expensive!)
DeepONet approach: Learn the operator once, then instant evaluation for any new source
Let's examine the existing Darcy implementation¶
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import diags
from scipy.sparse.linalg import spsolve
from scipy.stats import multivariate_normal
from tqdm import tqdm
# ========================= CELL 1: Data Generation =========================
def generate_darcy_data(n_funcs=1000, n_points=40):
"""Generate 1D nonlinear Darcy flow data"""
def permeability(s):
return 0.2 + s**2
# Gaussian process for source function
x = np.linspace(0, 1, n_points)
l, sigma = 0.04, 1.0
K = sigma**2 * np.exp(-0.5 * (x[:, None] - x[None, :])**2 / l**2)
K += 1e-6 * np.eye(n_points)
def solve_darcy(u_func):
dx = x[1] - x[0]
s = np.zeros(n_points)
for _ in range(100): # Fixed point iteration
kappa = permeability(s)
main_diag = (kappa[1:] + kappa[:-1]) / dx**2
upper_diag = -kappa[1:-1] / dx**2
lower_diag = -kappa[1:-1] / dx**2
A = diags([lower_diag, main_diag, upper_diag], [-1, 0, 1],
shape=(n_points-2, n_points-2))
s_interior = spsolve(A, u_func[1:-1])
s_new = np.zeros(n_points)
s_new[1:-1] = s_interior
s = 0.5 * s_new + 0.5 * s
return s
# Generate dataset
np.random.seed(42)
X, U, S = [], [], []
print("Generating Darcy flow dataset...")
for i in tqdm(range(n_funcs), desc="Solving PDEs"):
u = multivariate_normal.rvs(mean=np.zeros(n_points), cov=K)
s = solve_darcy(u)
X.append(x)
U.append(u)
S.append(s)
X = torch.tensor(np.array(X), dtype=torch.float32)
U = torch.tensor(np.array(U), dtype=torch.float32)
S = torch.tensor(np.array(S), dtype=torch.float32)
print(f"Dataset generated: {n_funcs} functions, {n_points} points each")
print(f"Input shape: {U.shape}, Output shape: {S.shape}")
return X, U, S
print("=== DATA GENERATION ===")
X, U, S = generate_darcy_data(n_funcs=1000, n_points=40)
# Plot samples
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
for i in range(6):
ax = axes[i//3, i%3]
ax.plot(X[i], U[i], 'g-', label='Source f(x)', linewidth=2)
ax.plot(X[i], S[i], 'b-', label='Solution u(x)', linewidth=2)
ax.set_title(f'Sample {i+1}')
ax.grid(True)
if i == 0:
ax.legend()
plt.tight_layout()
plt.savefig('darcy_samples.png', dpi=150)
plt.show()
=== DATA GENERATION === Generating Darcy flow dataset...
Solving PDEs: 100%|██████████| 1000/1000 [00:08<00:00, 121.29it/s]
Dataset generated: 1000 functions, 40 points each Input shape: torch.Size([1000, 40]), Output shape: torch.Size([1000, 40])
DeepONet Architecture¶
class DeepONet(nn.Module):
def __init__(self, branch_dim, trunk_dim, p_dim=128, hidden_dim=256):
super().__init__()
# Branch network (processes input function)
self.branch = nn.Sequential(
nn.Linear(branch_dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, p_dim)
)
# Trunk network (processes query points)
self.trunk = nn.Sequential(
nn.Linear(trunk_dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, p_dim)
)
def forward(self, u_vals, y_locs):
branch_out = self.branch(u_vals) # [batch, p_dim]
trunk_out = self.trunk(y_locs) # [batch, n_points, p_dim]
# Dot product: sum over p_dim
return torch.einsum('bp,bnp->bn', branch_out, trunk_out)
print("\n=== DEEPONET ARCHITECTURE ===")
print(f"Using device: {device}")
model = DeepONet(branch_dim=U.shape[1], trunk_dim=1, p_dim=128).to(device)
# Print model info
total_params = sum(p.numel() for p in model.parameters())
trainable_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"Total parameters: {total_params:,}")
print(f"Trainable parameters: {trainable_params:,}")
=== DEEPONET ARCHITECTURE === Using device: mps Total parameters: 208,384 Trainable parameters: 208,384
Training¶
def setup_training(X, U, S, model, device):
"""Prepare data and optimizer for training"""
# Split data
n_train = int(0.8 * len(U))
U_train, S_train = U[:n_train].to(device), S[:n_train].to(device)
U_test, S_test = U[n_train:].to(device), S[n_train:].to(device)
X_train, X_test = X[:n_train].to(device), X[n_train:].to(device)
# Normalize targets
S_mean, S_std = S_train.mean(), S_train.std()
S_train_norm = (S_train - S_mean) / S_std
S_test_norm = (S_test - S_mean) / S_std
print(f"Training samples: {len(U_train)}")
print(f"Test samples: {len(U_test)}")
print(f"Target normalization - Mean: {S_mean:.4f}, Std: {S_std:.4f}")
return (U_train, S_train_norm, X_train, U_test, S_test_norm, X_test, S_mean, S_std)
def train_model(model, train_data, epochs=5000, batch_size=64, lr=1e-3):
"""Train the DeepONet model"""
U_train, S_train_norm, X_train, _, _, _, _, _ = train_data
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=1e-5)
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=epochs)
print(f"Starting training: {epochs} epochs, batch size {batch_size}, lr {lr}")
model.train()
losses = []
pbar = tqdm(range(epochs), desc="Training")
for epoch in pbar:
# Random batch
idx = torch.randperm(len(U_train))[:batch_size]
u_batch = U_train[idx]
s_batch = S_train_norm[idx]
x_batch = X_train[idx].unsqueeze(-1) # [batch, n_points, 1]
# Forward pass
s_pred = model(u_batch, x_batch)
loss = F.mse_loss(s_pred, s_batch)
# Backward pass
optimizer.zero_grad()
loss.backward()
optimizer.step()
scheduler.step()
losses.append(loss.item())
if epoch % 100 == 0:
pbar.set_postfix({
'Loss': f'{loss.item():.6f}',
'LR': f'{scheduler.get_last_lr()[0]:.2e}'
})
print("Training completed!")
return losses
print("\n=== TRAINING ===")
train_data = setup_training(X, U, S, model, device)
losses = train_model(model, train_data, epochs=5000)
# Plot training loss
plt.figure(figsize=(10, 6))
plt.plot(losses)
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('MSE Loss')
plt.yscale('log')
plt.grid(True)
plt.savefig('training_loss.png', dpi=150)
plt.show()
=== TRAINING === Training samples: 800 Test samples: 200 Target normalization - Mean: -0.0046, Std: 0.1468 Starting training: 5000 epochs, batch size 64, lr 0.001
Training: 100%|██████████| 5000/5000 [00:24<00:00, 202.99it/s, Loss=0.001128, LR=9.67e-07]
Training completed!
DeepONet Prediction¶
def evaluate_model(model, train_data):
"""Evaluate model and create visualizations"""
U_train, S_train_norm, X_train, U_test, S_test_norm, X_test, S_mean, S_std = train_data
model.eval()
device = next(model.parameters()).device
with torch.no_grad():
# Test on first few samples
n_test = min(5, len(U_test))
u_test = U_test[:n_test]
s_test_norm = S_test_norm[:n_test]
x_test = X_test[:n_test].unsqueeze(-1)
# Predict
s_pred_norm = model(u_test, x_test)
# Denormalize
s_pred = s_pred_norm * S_std + S_mean
s_test = s_test_norm * S_std + S_mean
# Compute error
l2_error = torch.sqrt(torch.mean((s_pred - s_test)**2) / torch.mean(s_test**2))
print(f"Relative L2 error: {l2_error.item():.4f}")
return s_pred, s_test, u_test, X_test
print("\n=== PREDICTION & EVALUATION ===")
s_pred, s_test, u_test, X_test = evaluate_model(model, train_data)
# Plot results
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
for i in range(min(6, len(s_pred))):
ax = axes[i//3, i%3]
x_np = X_test[i].cpu().numpy()
ax.plot(x_np, s_test[i].cpu().numpy(), 'k-', label='True s(x)', linewidth=2)
ax.plot(x_np, s_pred[i].cpu().numpy(), 'r--', label='Pred s(x)', linewidth=2)
ax.set_title(f'Test Sample {i+1}')
ax.grid(True)
if i == 0:
ax.legend()
plt.tight_layout()
plt.savefig('deeponet_results.png', dpi=150)
plt.show()
=== PREDICTION & EVALUATION === Relative L2 error: 0.0306
Understanding basis functions¶
def extract_basis_functions(model, X_test):
"""Extract and visualize learned basis functions"""
device = next(model.parameters()).device
model.eval()
with torch.no_grad():
# Use test locations
x_points = X_test[0].unsqueeze(0).unsqueeze(-1).to(device) # [1, n_points, 1]
# Get trunk network output (basis functions)
trunk_out = model.trunk(x_points) # [1, n_points, p_dim]
basis_functions = trunk_out.squeeze(0).cpu().numpy() # [n_points, p_dim]
print(f"Extracted {basis_functions.shape[1]} basis functions")
print(f"Each basis function has {basis_functions.shape[0]} points")
return basis_functions
print("\n=== BASIS FUNCTION ANALYSIS ===")
basis_functions = extract_basis_functions(model, X_test)
# Plot first 8 basis functions
fig, axes = plt.subplots(2, 4, figsize=(16, 8))
x_np = X_test[0].cpu().numpy()
for i in range(8):
ax = axes[i//4, i%4]
ax.plot(x_np, basis_functions[:, i], 'b-', linewidth=2)
ax.set_title(f'Basis Function φ_{i+1}(y)')
ax.grid(True)
ax.set_xlabel('y')
plt.tight_layout()
plt.savefig('basis_functions.png', dpi=150)
plt.show()
=== BASIS FUNCTION ANALYSIS === Extracted 128 basis functions Each basis function has 40 points
Summary:¶
What We've Learned¶
Conceptual Leap: From function approximation to operator learning
- Functions: $\mathbb{R}^d \rightarrow \mathbb{R}^m$ (point to point)
- Operators: $\mathcal{F}_1 \rightarrow \mathcal{F}_2$ (function to function)
Theoretical Foundation: Universal Approximation Theorem for Operators
- Neural networks can approximate operators!
- Branch-trunk architecture emerges naturally
- Basis function decomposition: $\mathcal{G}(u)(y) = \sum_k b_k(u) \cdot t_k(y)$
Practical Implementation: DeepONet architecture
- Branch network: Encodes input functions into coefficients
- Trunk network: Generates basis functions at query points
- Training: Learn from input-output function pairs
Real Applications: From derivatives to nonlinear PDEs
- Derivative operator: Perfect pedagogical example
- Darcy flow: Real-world nonlinear PDE
- Generalization: Works on unseen function types
Key Advantages of DeepONet¶
✅ Resolution independence: Train on one grid, evaluate on any grid
✅ Fast evaluation: Once trained, instant prediction
✅ Generalization: Works for new functions not seen during training
✅ Physical consistency: Learns the underlying operator, not just patterns
When to Use DeepONet¶
Ideal scenarios:
- Parametric PDEs: Need solutions for many different source terms/boundary conditions
- Real-time applications: Require instant evaluation
- Complex geometries: Traditional methods struggle
- Multi-query problems: Same operator, many evaluations
Limitations:
- Training data: Need many solved examples
- Complex operators: Very nonlinear mappings may be challenging
- High dimensions: Curse of dimensionality still applies
The Bigger Picture¶
DeepONet represents a paradigm shift:
- Traditional numerical methods: Solve each problem instance
- Operator learning: Learn the solution pattern once, apply everywhere
This opens new possibilities for:
- Inverse problems: Learn parameter-to-solution mappings
- Control applications: Real-time system response
- Multi-physics: Coupled operator learning
- Scientific discovery: Understanding operator structure
Next: Combine with PINNs for physics-informed operator learning!
Further Reading and Extensions¶
Key Papers¶
- Lu et al. (2019) - Original DeepONet paper
- Goswami et al. (2023) - Physics-informed DeepONets
- Chen & Chen (1995) - Universal approximation theorem for operators
Extensions to Explore¶
- Multi-output operators: Vector-valued mappings
- Higher dimensions: 2D/3D PDEs
- Physics-informed training: Incorporate governing equations
- Fourier Neural Operators: Alternative operator learning architecture
Exercises¶
- Modify the derivative example to learn the second derivative operator
- Extend to 2D by implementing the Laplacian operator $\nabla^2 u$
- Add physics constraints by incorporating the differential equation into the loss
- Compare with traditional methods on computational efficiency
The journey from function approximation to operator learning represents one of the most exciting frontiers in scientific machine learning!
