Differentiable Simulation¶
Exercise: 
Slides:
In the previous MLP notebook, we introduced Automatic Differentiation (AD) as the core engine that enables the training of neural networks by computing gradients of a loss function with respect to network parameters.
However, the power of AD extends far beyond just neural networks. It allows us to make entire physical simulations differentiable. This paradigm, often called Differentiable Simulation or Differentiable Physics, involves implementing a simulator (e.g., a PDE solver) in a framework that supports AD, such as PyTorch or JAX. By doing so, we can automatically compute the gradient of a final quantity (like a measurement or a loss function) with respect to any initial parameter of the simulation.
This notebook demonstrates this powerful concept. We will:
- Briefly recall how gradients are computed in PyTorch.
- Introduce the JAX framework for high-performance differentiable programming.
- Build a differentiable simulator for the 1D acoustic wave equation.
- Use this simulator to solve a challenging inverse problem: Full Waveform Inversion (FWI).
What is Differentiable Simulation?¶
Differentiable simulation combines physics-based simulation with automatic differentiation to solve inverse problems.
Instead of:
- Forward Problem: Given parameters → predict observations
- Traditional Inverse: Trial-and-error parameter search
We use:
- Differentiable Simulation: Compute gradients through simulation → gradient-based optimization
Key insight: If we can compute $\frac{\partial \text{simulation}}{\partial \text{parameters}}$, we can use gradient descent to find optimal parameters.
From PyTorch to JAX: A Quick Review¶
We introduced automatic differentiation in the MLP module.
As we saw previously, frameworks like PyTorch keep track of all operations on tensors. When we call .backward() on a final scalar output (like a loss), PyTorch uses reverse-mode AD (backpropagation) to compute the gradient of that output with respect to the inputs that have requires_grad=True. Here's a quick recap of computing gradients in PyTorch:
In [1]:
Copied!
import torch
import numpy as np
import matplotlib.pyplot as plt
# Simple function: loss = (prediction - target)^2
def simple_loss(params, target):
prediction = params[0] * 2.0 + params[1] # ax + b
return (prediction - target)**2
# PyTorch gradient computation
params = torch.tensor([1.0, 0.5], requires_grad=True)
target = 5.0
loss = simple_loss(params, target)
loss.backward()
print(f"Loss: {loss.item():.4f}")
print(f"Gradients: {params.grad}")
print(f"Parameters: {params.detach()}")
import torch
import numpy as np
import matplotlib.pyplot as plt
# Simple function: loss = (prediction - target)^2
def simple_loss(params, target):
prediction = params[0] * 2.0 + params[1] # ax + b
return (prediction - target)**2
# PyTorch gradient computation
params = torch.tensor([1.0, 0.5], requires_grad=True)
target = 5.0
loss = simple_loss(params, target)
loss.backward()
print(f"Loss: {loss.item():.4f}")
print(f"Gradients: {params.grad}")
print(f"Parameters: {params.detach()}")
Loss: 6.2500 Gradients: tensor([-10., -5.]) Parameters: tensor([1.0000, 0.5000])
JAX: The Scientific Computing Advantage¶
JAX provides several advantages for scientific computing:
- Functional programming: Pure functions, no side effects
- JIT compilation: Fast execution with
jit - Vectorization: Automatic batching with
vmap - Transformations:
grad,jit,vmapcompose seamlessly
Same computation in JAX:
In [2]:
Copied!
!pip install -q jax jaxlib optax tensorflow-probability
!pip install -q jax jaxlib optax tensorflow-probability
In [3]:
Copied!
import jax
import jax.numpy as jnp
from jax import grad, jit, vmap, lax
import optax
import matplotlib.pyplot as plt
from tensorflow_probability.substrates import jax as tfp
# Same function in JAX
def simple_loss_jax(params, target):
prediction = params[0] * 2.0 + params[1]
return (prediction - target)**2
# JAX gradient computation
params_jax = jnp.array([1.0, 0.5])
target_jax = 5.0
# Create gradient function
grad_fn = grad(simple_loss_jax)
loss_val = simple_loss_jax(params_jax, target_jax)
gradients = grad_fn(params_jax, target_jax)
print(f"Loss: {loss_val:.4f}")
print(f"Gradients: {gradients}")
print(f"Parameters: {params_jax}")
import jax
import jax.numpy as jnp
from jax import grad, jit, vmap, lax
import optax
import matplotlib.pyplot as plt
from tensorflow_probability.substrates import jax as tfp
# Same function in JAX
def simple_loss_jax(params, target):
prediction = params[0] * 2.0 + params[1]
return (prediction - target)**2
# JAX gradient computation
params_jax = jnp.array([1.0, 0.5])
target_jax = 5.0
# Create gradient function
grad_fn = grad(simple_loss_jax)
loss_val = simple_loss_jax(params_jax, target_jax)
gradients = grad_fn(params_jax, target_jax)
print(f"Loss: {loss_val:.4f}")
print(f"Gradients: {gradients}")
print(f"Parameters: {params_jax}")
Loss: 6.2500 Gradients: [-10. -5.] Parameters: [1. 0.5]
In [4]:
Copied!
import jax.numpy as jnp
from jax import jit, grad
import time
# Complex polynomial operation
def f(x):
return x**4 - 3*x**3 + 2*x**2 - x + 1
# JIT version
@jit
def fast_f(x):
return x**4 - 3*x**3 + 2*x**2 - x + 1
# Large array
x = jnp.linspace(-10, 10, 1_000_000)
# Time without JIT
start = time.time()
result1 = f(x)
time_no_jit = time.time() - start
# Time with JIT (includes compilation on first run)
start = time.time()
result2 = fast_f(x)
time_with_jit = time.time() - start
# Time JIT on second run (no compilation)
start = time.time()
result3 = fast_f(x)
time_jit_second = time.time() - start
print(f"No JIT: {time_no_jit:.4f}s")
print(f"JIT (first run): {time_with_jit:.4f}s")
print(f"JIT (second run): {time_jit_second:.4f}s")
print(f"Speedup: {time_no_jit/time_jit_second:.2f}x")
# Gradient example
df = grad(f)
fast_df = jit(grad(f))
print(f"Gradient at x=1.0: {df(1.0)}")
print(f"JIT gradient at x=1.0: {fast_df(1.0)}")
import jax.numpy as jnp
from jax import jit, grad
import time
# Complex polynomial operation
def f(x):
return x**4 - 3*x**3 + 2*x**2 - x + 1
# JIT version
@jit
def fast_f(x):
return x**4 - 3*x**3 + 2*x**2 - x + 1
# Large array
x = jnp.linspace(-10, 10, 1_000_000)
# Time without JIT
start = time.time()
result1 = f(x)
time_no_jit = time.time() - start
# Time with JIT (includes compilation on first run)
start = time.time()
result2 = fast_f(x)
time_with_jit = time.time() - start
# Time JIT on second run (no compilation)
start = time.time()
result3 = fast_f(x)
time_jit_second = time.time() - start
print(f"No JIT: {time_no_jit:.4f}s")
print(f"JIT (first run): {time_with_jit:.4f}s")
print(f"JIT (second run): {time_jit_second:.4f}s")
print(f"Speedup: {time_no_jit/time_jit_second:.2f}x")
# Gradient example
df = grad(f)
fast_df = jit(grad(f))
print(f"Gradient at x=1.0: {df(1.0)}")
print(f"JIT gradient at x=1.0: {fast_df(1.0)}")
No JIT: 0.0841s JIT (first run): 0.0156s JIT (second run): 0.0000s Speedup: 1789.65x Gradient at x=1.0: -2.0 JIT gradient at x=1.0: -2.0
JAX Transformations: The Power of Composition¶
JAX's key advantage is that transformations compose. You can combine grad, jit, and vmap in any order:
In [5]:
Copied!
# vmap example - scalar function that needs vectorization
from jax import vmap
def scalar_only_func(x):
"""Function that only works on scalars"""
return jnp.where(x > 0, x**2, -x**3)
# This would fail on array: scalar_only_func(x)
# Need vmap to vectorize it
vectorized_func = vmap(scalar_only_func)
jit_vectorized_func = jit(vmap(scalar_only_func))
# Test on smaller array
small_x = jnp.array([-2.0, -1.0, 0.0, 1.0, 2.0])
result_vmap = vectorized_func(small_x)
result_jit_vmap = jit_vectorized_func(small_x)
print(f"vmap result: {result_vmap}")
print(f"jit+vmap result: {result_jit_vmap}")
# vmap example - scalar function that needs vectorization
from jax import vmap
def scalar_only_func(x):
"""Function that only works on scalars"""
return jnp.where(x > 0, x**2, -x**3)
# This would fail on array: scalar_only_func(x)
# Need vmap to vectorize it
vectorized_func = vmap(scalar_only_func)
jit_vectorized_func = jit(vmap(scalar_only_func))
# Test on smaller array
small_x = jnp.array([-2.0, -1.0, 0.0, 1.0, 2.0])
result_vmap = vectorized_func(small_x)
result_jit_vmap = jit_vectorized_func(small_x)
print(f"vmap result: {result_vmap}")
print(f"jit+vmap result: {result_jit_vmap}")
vmap result: [ 8. 1. -0. 1. 4.] jit+vmap result: [ 8. 1. -0. 1. 4.]
The 1D Wave Equation: Our Physics Model¶
Let's implement a differentiable physics simulation. We'll use the 1D acoustic wave equation:
$$\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}$$
Where:
- $u(x,t)$ is the wavefield (pressure/displacement)
- $c(x)$ is the wave speed (what we want to estimate)
Finite difference discretization: $$u_{i}^{n+1} = 2u_{i}^{n} - u_{i}^{n-1} + \frac{c_i^2 \Delta t^2}{\Delta x^2}(u_{i+1}^{n} - 2u_{i}^{n} + u_{i-1}^{n})$$
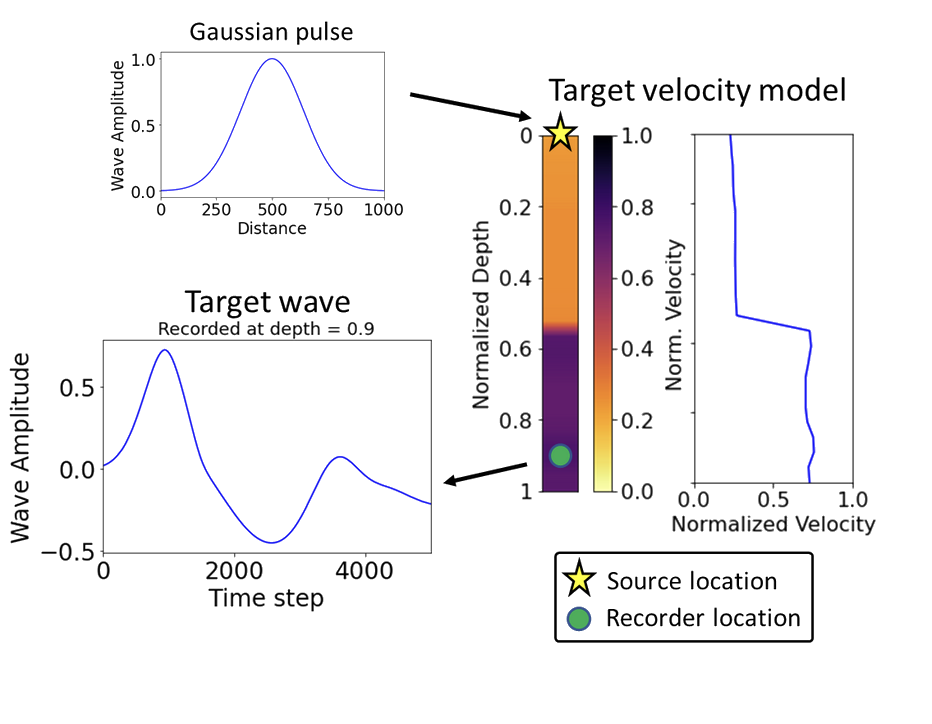
Initial conditions: Gaussian source $$u_0 = \exp\left(-5(x - 0.5)^2\right)$$
The Forward Problem: Simulation¶
The forward problem is to simulate the behavior of $u(x,t)$ given an initial state and the wave speed profile $c(x)$. We will solve this using a finite difference method. By rearranging the central difference approximation, we can find the wave's state at the next timestep based on its two previous states:
$$u_i^{n+1} = c_i^2 \frac{\Delta t^2}{\Delta x^2} (u_{i+1}^n - 2u_i^n + u_{i-1}^n) + 2u_i^n - u_i^{n-1} $$
We can implement this time-stepping loop in JAX. Using @jit, this loop will be compiled for high performance.
In [6]:
Copied!
# Set up the wave equation solver
n = 1000 # Number of spatial points
dx = 1.0 / (n - 1)
x0 = jnp.linspace(0.0, 1.0, n)
@jit
def wave_propagation(params):
"""Solve 1D wave equation using finite differences"""
c = params # Velocity model
dt = 5e-4 # Time step
# CFL condition check: C = c*dt/dx should be < 1
C = c * dt / dx
C2 = C * C
# Initial conditions: Gaussian source
u0 = jnp.exp(-(5 * (x0 - 0.5))**2)
u1 = jnp.exp(-(5 * (x0 - 0.5 - c * dt))**2)
u2 = jnp.zeros(n)
def step(i, carry):
u0, u1, u2 = carry
# Boundary conditions: u = 0 at boundaries
u1p = jnp.roll(u1, 1).at[0].set(0) # u[j-1]
u1n = jnp.roll(u1, -1).at[n-1].set(0) # u[j+1]
# Central difference scheme
u2 = 2 * u1 - u0 + C2 * (u1p - 2 * u1 + u1n)
# Update for next iteration
u0 = u1
u1 = u2
return (u0, u1, u2)
# Time stepping: 5000 steps
u0, u1, u2 = lax.fori_loop(0, 5000, step, (u0, u1, u2))
return u2
print("Wave propagation solver defined successfully!")
print(f"Grid points: {n}")
print(f"Spatial step: {dx:.6f}")
print(f"Time step: {5e-4}")
# Set up the wave equation solver
n = 1000 # Number of spatial points
dx = 1.0 / (n - 1)
x0 = jnp.linspace(0.0, 1.0, n)
@jit
def wave_propagation(params):
"""Solve 1D wave equation using finite differences"""
c = params # Velocity model
dt = 5e-4 # Time step
# CFL condition check: C = c*dt/dx should be < 1
C = c * dt / dx
C2 = C * C
# Initial conditions: Gaussian source
u0 = jnp.exp(-(5 * (x0 - 0.5))**2)
u1 = jnp.exp(-(5 * (x0 - 0.5 - c * dt))**2)
u2 = jnp.zeros(n)
def step(i, carry):
u0, u1, u2 = carry
# Boundary conditions: u = 0 at boundaries
u1p = jnp.roll(u1, 1).at[0].set(0) # u[j-1]
u1n = jnp.roll(u1, -1).at[n-1].set(0) # u[j+1]
# Central difference scheme
u2 = 2 * u1 - u0 + C2 * (u1p - 2 * u1 + u1n)
# Update for next iteration
u0 = u1
u1 = u2
return (u0, u1, u2)
# Time stepping: 5000 steps
u0, u1, u2 = lax.fori_loop(0, 5000, step, (u0, u1, u2))
return u2
print("Wave propagation solver defined successfully!")
print(f"Grid points: {n}")
print(f"Spatial step: {dx:.6f}")
print(f"Time step: {5e-4}")
Wave propagation solver defined successfully! Grid points: 1000 Spatial step: 0.001001 Time step: 0.0005
Example 1: Constant Velocity Recovery¶
The Problem: Given observed wavefield data, can we recover a constant velocity?
- Target: $c = 1.0$ (constant)
- Initial guess: $c = 0.8$
- Goal: Use gradients to optimize $c$ until simulation matches observations
In [7]:
Copied!
# Generate synthetic observed data
ctarget = 1.0 # True constant velocity
target_data = wave_propagation(ctarget)
# Visualize target
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x0, jnp.ones(n) * ctarget, 'c-', linewidth=3, label='Target velocity')
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('Target Velocity Model')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
plt.plot(x0, target_data, 'b-', linewidth=2, label='Target wavefield')
plt.xlabel('Position')
plt.ylabel('Amplitude')
plt.title('Target Wavefield Data')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"Target velocity: {ctarget}")
print(f"Target data shape: {target_data.shape}")
# Generate synthetic observed data
ctarget = 1.0 # True constant velocity
target_data = wave_propagation(ctarget)
# Visualize target
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x0, jnp.ones(n) * ctarget, 'c-', linewidth=3, label='Target velocity')
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('Target Velocity Model')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
plt.plot(x0, target_data, 'b-', linewidth=2, label='Target wavefield')
plt.xlabel('Position')
plt.ylabel('Amplitude')
plt.title('Target Wavefield Data')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"Target velocity: {ctarget}")
print(f"Target data shape: {target_data.shape}")
Target velocity: 1.0 Target data shape: (1000,)
In [8]:
Copied!
# Define loss function for constant velocity inversion
@jit
def compute_loss_constant(c_scalar):
"""Loss function for constant velocity model"""
# Convert scalar to constant array
c_array = jnp.ones(n) * c_scalar
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_data)
# Gradient function
grad_loss_constant = jit(grad(compute_loss_constant))
# Initial guess
c_initial = 0.8
print(f"Initial guess: {c_initial}")
print(f"Target: {ctarget}")
print(f"Initial loss: {compute_loss_constant(c_initial):.6f}")
# Define loss function for constant velocity inversion
@jit
def compute_loss_constant(c_scalar):
"""Loss function for constant velocity model"""
# Convert scalar to constant array
c_array = jnp.ones(n) * c_scalar
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_data)
# Gradient function
grad_loss_constant = jit(grad(compute_loss_constant))
# Initial guess
c_initial = 0.8
print(f"Initial guess: {c_initial}")
print(f"Target: {ctarget}")
print(f"Initial loss: {compute_loss_constant(c_initial):.6f}")
Initial guess: 0.8 Target: 1.0 Initial loss: 15.758533
In [9]:
Copied!
# Optimize constant velocity using Adam
def optax_adam_constant(c_init, niter):
"""Optimize constant velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
c_param = c_init
opt_state = optimizer.init(c_param)
losses = []
for i in range(niter):
loss_val = compute_loss_constant(c_param)
grads = grad_loss_constant(c_param)
updates, opt_state = optimizer.update(grads, opt_state)
c_param = optax.apply_updates(c_param, updates)
losses.append(loss_val)
if i % 200 == 0:
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity = {c_param:.6f}")
return c_param, losses
# Run optimization
print("Starting constant velocity optimization...")
c_optimized, losses = optax_adam_constant(c_initial, 1000)
print(f"\nOptimization Results:")
print(f"Initial velocity: {c_initial:.6f}")
print(f"Target velocity: {ctarget:.6f}")
print(f"Final velocity: {c_optimized:.6f}")
print(f"Error: {abs(c_optimized - ctarget):.6f}")
print(f"Loss reduction: {losses[0]/losses[-1]:.1f}x")
# Optimize constant velocity using Adam
def optax_adam_constant(c_init, niter):
"""Optimize constant velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
c_param = c_init
opt_state = optimizer.init(c_param)
losses = []
for i in range(niter):
loss_val = compute_loss_constant(c_param)
grads = grad_loss_constant(c_param)
updates, opt_state = optimizer.update(grads, opt_state)
c_param = optax.apply_updates(c_param, updates)
losses.append(loss_val)
if i % 200 == 0:
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity = {c_param:.6f}")
return c_param, losses
# Run optimization
print("Starting constant velocity optimization...")
c_optimized, losses = optax_adam_constant(c_initial, 1000)
print(f"\nOptimization Results:")
print(f"Initial velocity: {c_initial:.6f}")
print(f"Target velocity: {ctarget:.6f}")
print(f"Final velocity: {c_optimized:.6f}")
print(f"Error: {abs(c_optimized - ctarget):.6f}")
print(f"Loss reduction: {losses[0]/losses[-1]:.1f}x")
Starting constant velocity optimization... Iteration 0: Loss = 15.758533, Velocity = 0.801000 Iteration 200: Loss = 0.039644, Velocity = 1.000228 Iteration 400: Loss = 0.021305, Velocity = 1.000039 Iteration 600: Loss = 0.021443, Velocity = 1.000031 Iteration 800: Loss = 0.017808, Velocity = 1.000041 Optimization Results: Initial velocity: 0.800000 Target velocity: 1.000000 Final velocity: 0.999937 Error: 0.000063 Loss reduction: 840.8x
Example 2: Linear profile¶
In [10]:
Copied!
# Generate synthetic data for linear velocity profile
ctarget_linear = jnp.linspace(0.9, 1.0, n) # Target: linear increase
target_linear = wave_propagation(ctarget_linear)
# Initial guess: different linear profile
c_initial_linear = jnp.linspace(0.85, 1.0, n)
# Define loss function for linear velocity profile
@jit
def compute_loss_linear(c_array):
"""Loss function for spatially-varying velocity model"""
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_linear)
# Gradient function
grad_loss_linear = jit(grad(compute_loss_linear))
# Visualize setup
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x0, ctarget_linear, 'r-', linewidth=3, label='Target velocity')
plt.plot(x0, c_initial_linear, 'b--', linewidth=2, label='Initial guess')
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('Linear Velocity Profiles')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
target_init_linear = wave_propagation(c_initial_linear)
plt.plot(x0, target_linear, 'r-', linewidth=2, label='Target wavefield')
plt.plot(x0, target_init_linear, 'b--', linewidth=2, label='Initial wavefield')
plt.xlabel('Position')
plt.ylabel('Amplitude')
plt.title('Wavefield Comparison')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"Target velocity range: [{jnp.min(ctarget_linear):.3f}, {jnp.max(ctarget_linear):.3f}]")
print(f"Initial guess range: [{jnp.min(c_initial_linear):.3f}, {jnp.max(c_initial_linear):.3f}]")
print(f"Number of parameters to optimize: {len(c_initial_linear)}")
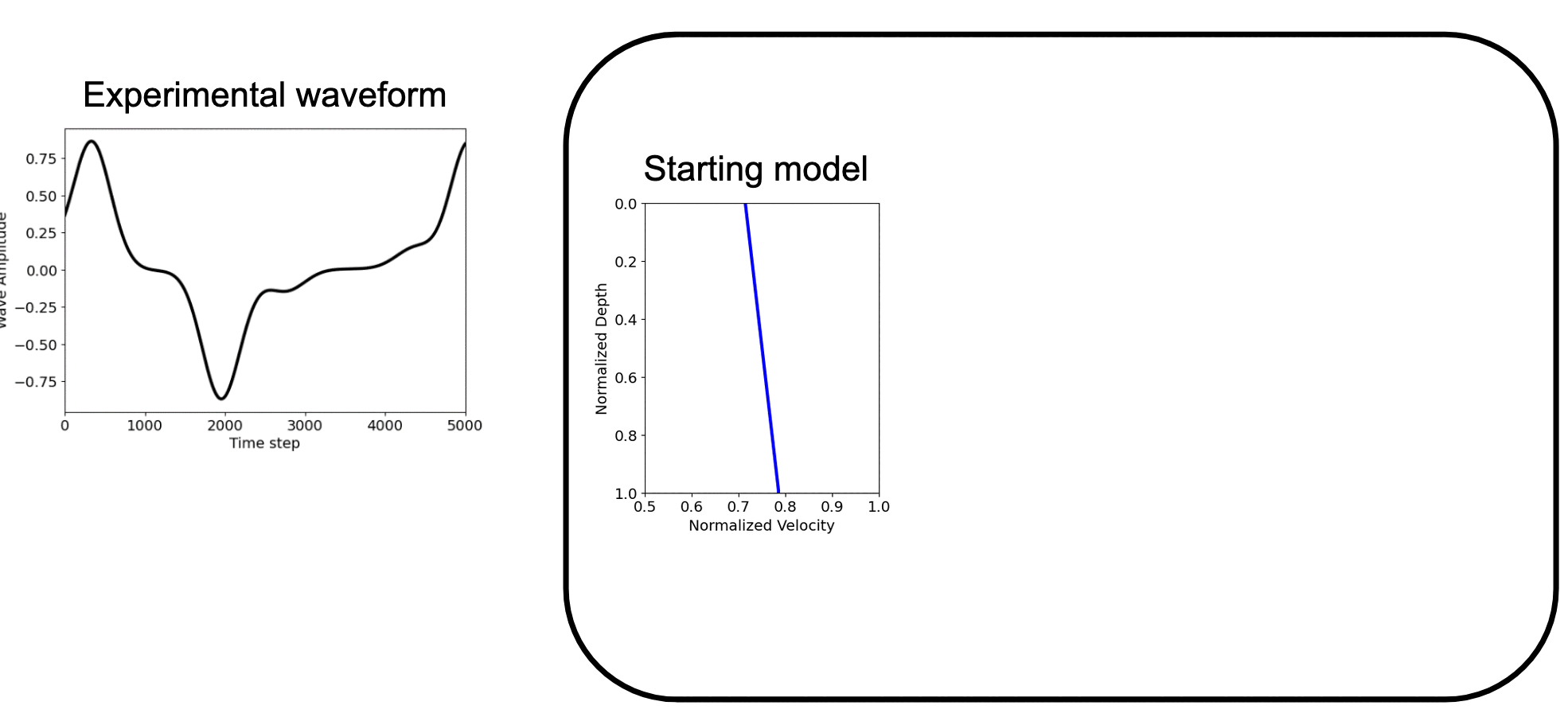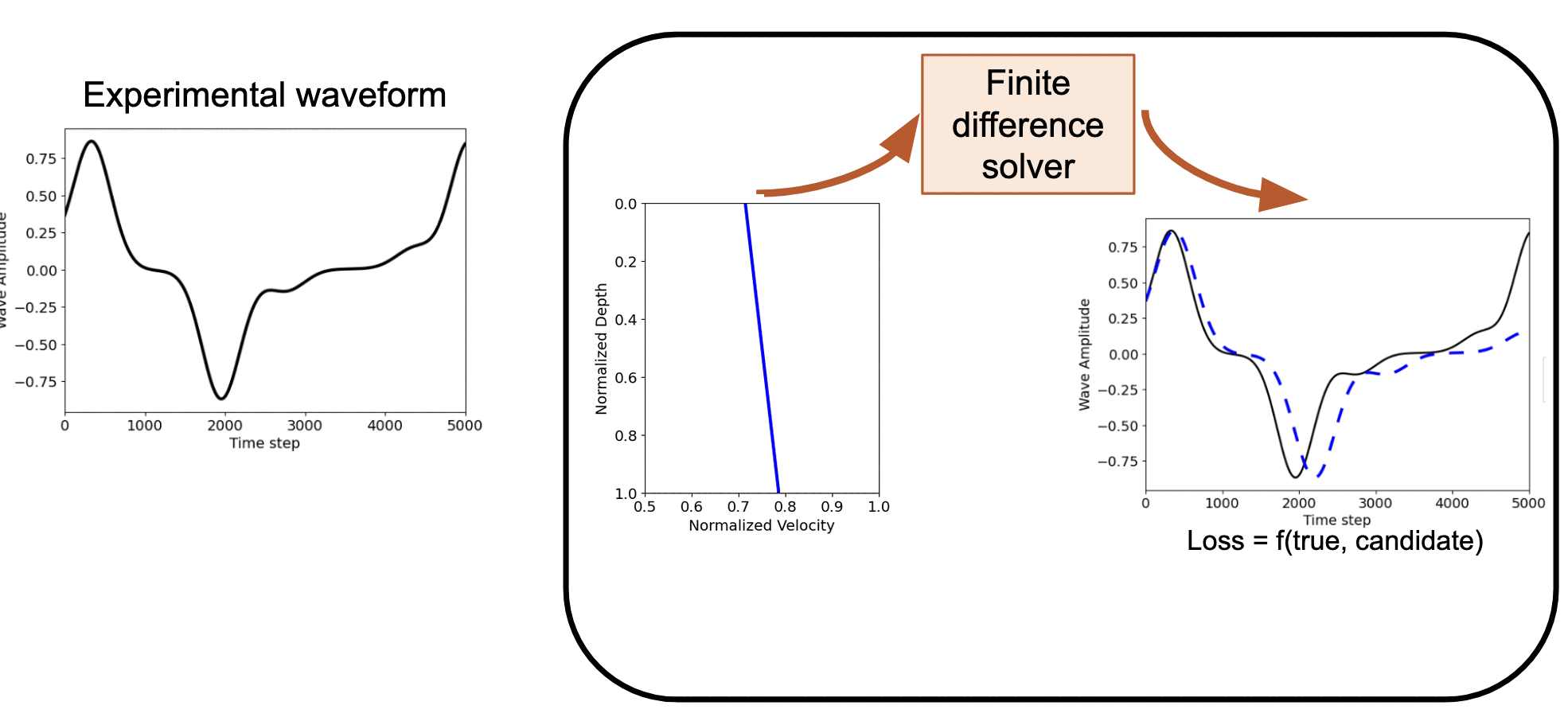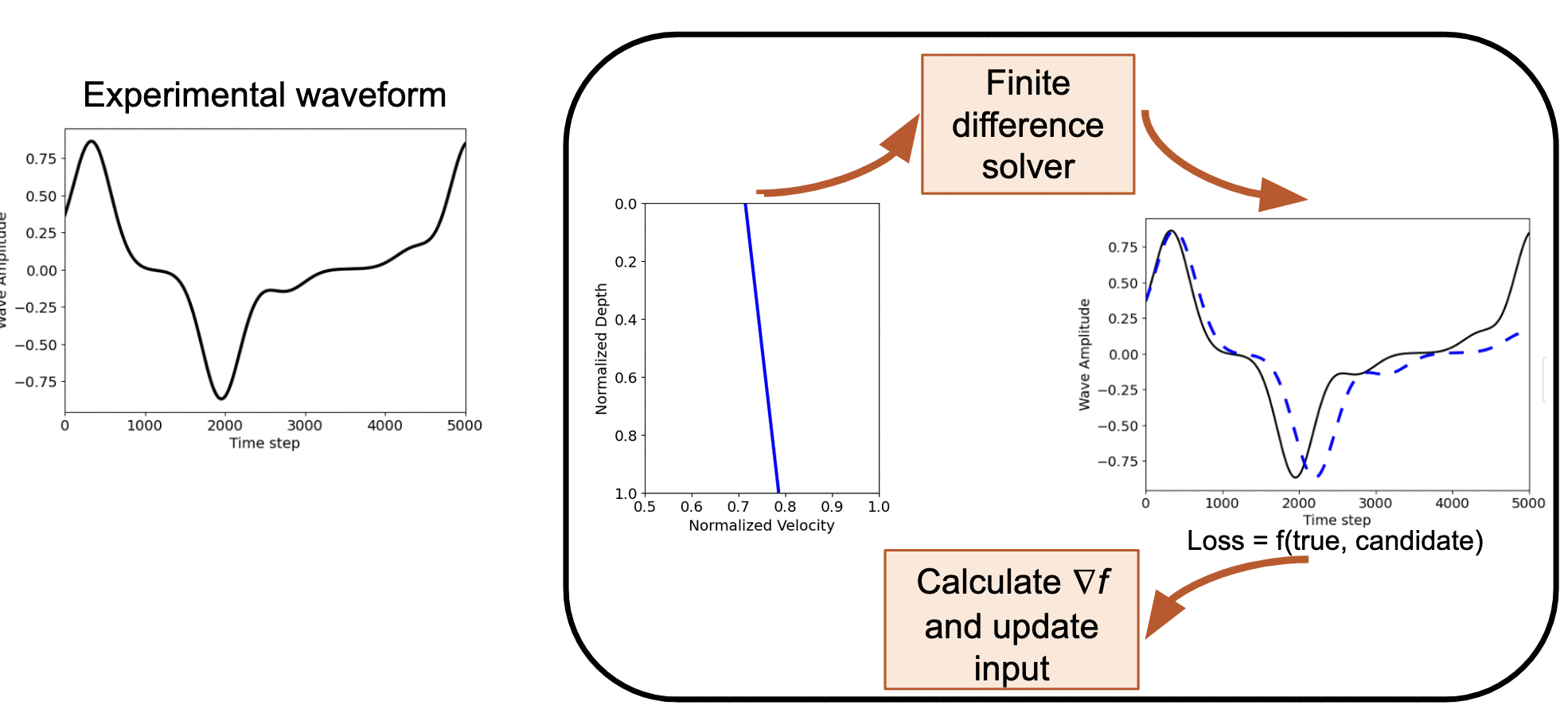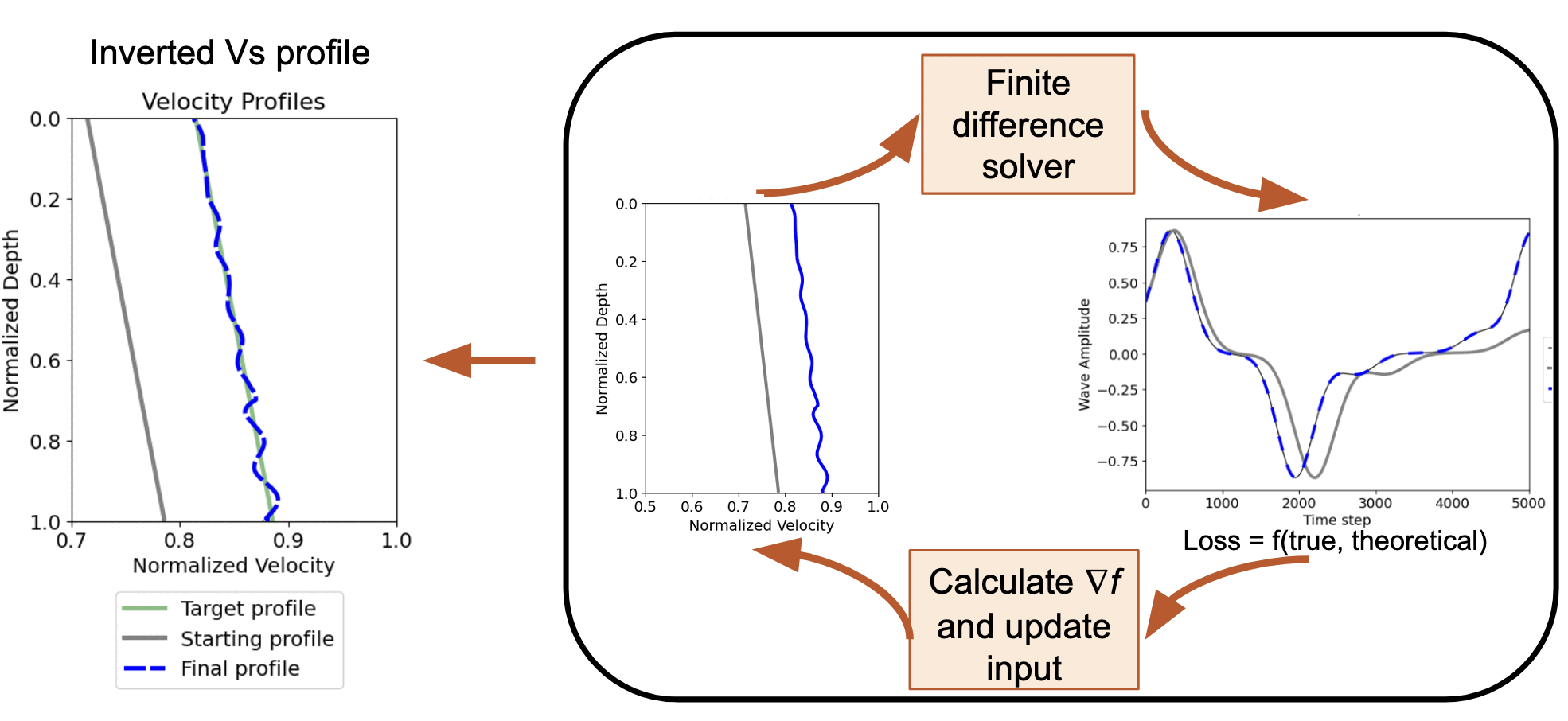
# Generate synthetic data for linear velocity profile
ctarget_linear = jnp.linspace(0.9, 1.0, n) # Target: linear increase
target_linear = wave_propagation(ctarget_linear)
# Initial guess: different linear profile
c_initial_linear = jnp.linspace(0.85, 1.0, n)
# Define loss function for linear velocity profile
@jit
def compute_loss_linear(c_array):
"""Loss function for spatially-varying velocity model"""
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_linear)
# Gradient function
grad_loss_linear = jit(grad(compute_loss_linear))
# Visualize setup
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x0, ctarget_linear, 'r-', linewidth=3, label='Target velocity')
plt.plot(x0, c_initial_linear, 'b--', linewidth=2, label='Initial guess')
plt.xlabel('Position')
plt.ylabel('Velocity')
plt.title('Linear Velocity Profiles')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
target_init_linear = wave_propagation(c_initial_linear)
plt.plot(x0, target_linear, 'r-', linewidth=2, label='Target wavefield')
plt.plot(x0, target_init_linear, 'b--', linewidth=2, label='Initial wavefield')
plt.xlabel('Position')
plt.ylabel('Amplitude')
plt.title('Wavefield Comparison')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"Target velocity range: [{jnp.min(ctarget_linear):.3f}, {jnp.max(ctarget_linear):.3f}]")
print(f"Initial guess range: [{jnp.min(c_initial_linear):.3f}, {jnp.max(c_initial_linear):.3f}]")
print(f"Number of parameters to optimize: {len(c_initial_linear)}")
Target velocity range: [0.900, 1.000] Initial guess range: [0.850, 1.000] Number of parameters to optimize: 1000
In [11]:
Copied!
# Test initial loss and gradient to verify everything is working
initial_loss_linear = compute_loss_linear(c_initial_linear)
initial_grad_linear = grad_loss_linear(c_initial_linear)
print(f"Initial loss: {initial_loss_linear:.6f}")
print(f"Gradient shape: {initial_grad_linear.shape}")
print(f"Gradient norm: {jnp.linalg.norm(initial_grad_linear):.6f}")
print(f"Gradient range: [{jnp.min(initial_grad_linear):.6f}, {jnp.max(initial_grad_linear):.6f}]")
# Test initial loss and gradient to verify everything is working
initial_loss_linear = compute_loss_linear(c_initial_linear)
initial_grad_linear = grad_loss_linear(c_initial_linear)
print(f"Initial loss: {initial_loss_linear:.6f}")
print(f"Gradient shape: {initial_grad_linear.shape}")
print(f"Gradient norm: {jnp.linalg.norm(initial_grad_linear):.6f}")
print(f"Gradient range: [{jnp.min(initial_grad_linear):.6f}, {jnp.max(initial_grad_linear):.6f}]")
Initial loss: 3.944904 Gradient shape: (1000,) Gradient norm: 4.976274 Gradient range: [-0.264329, -0.000011]
In [12]:
Copied!
# Optimizers for linear profile
def optax_adam_linear(params, niter):
"""Optimize spatially-varying velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
opt_state = optimizer.init(params)
for i in range(niter):
grads = grad_loss_linear(params)
updates, opt_state = optimizer.update(grads, opt_state)
params = optax.apply_updates(params, updates)
if i % 200 == 0:
loss_val = compute_loss_linear(params)
velocity_rmse = jnp.sqrt(jnp.mean((params - ctarget_linear)**2))
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity RMSE = {velocity_rmse:.6f}")
return params
def tfp_lbfgs_linear(params):
"""Optimize using L-BFGS"""
# For TFP L-BFGS, we need a function that returns both value and gradients
from jax import value_and_grad
value_and_grad_fn = jit(value_and_grad(compute_loss_linear))
results = tfp.optimizer.lbfgs_minimize(
value_and_grad_fn,
initial_position=params,
tolerance=1e-5
)
return results.position
# Initial and Target
c_initial_linear = jnp.linspace(0.85, 1.0, n)
ctarget_linear = jnp.linspace(0.9, 1.0, n)
# Run Adam optimization
print("Starting Adam optimization...")
result_adam = optax_adam_linear(c_initial_linear, 1000)
# Run L-BFGS optimization
print("\nStarting L-BFGS optimization...")
result_lbfgs = tfp_lbfgs_linear(c_initial_linear)
# Compare results
adam_rmse = jnp.sqrt(jnp.mean((result_adam - ctarget_linear)**2))
lbfgs_rmse = jnp.sqrt(jnp.mean((result_lbfgs - ctarget_linear)**2))
print(f"\nFinal Results:")
print(f"Adam RMSE: {adam_rmse:.8f}")
print(f"L-BFGS RMSE: {lbfgs_rmse:.8f}")
print(f"L-BFGS improvement: {adam_rmse/lbfgs_rmse:.1f}x better")
# Optimizers for linear profile
def optax_adam_linear(params, niter):
"""Optimize spatially-varying velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
opt_state = optimizer.init(params)
for i in range(niter):
grads = grad_loss_linear(params)
updates, opt_state = optimizer.update(grads, opt_state)
params = optax.apply_updates(params, updates)
if i % 200 == 0:
loss_val = compute_loss_linear(params)
velocity_rmse = jnp.sqrt(jnp.mean((params - ctarget_linear)**2))
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity RMSE = {velocity_rmse:.6f}")
return params
def tfp_lbfgs_linear(params):
"""Optimize using L-BFGS"""
# For TFP L-BFGS, we need a function that returns both value and gradients
from jax import value_and_grad
value_and_grad_fn = jit(value_and_grad(compute_loss_linear))
results = tfp.optimizer.lbfgs_minimize(
value_and_grad_fn,
initial_position=params,
tolerance=1e-5
)
return results.position
# Initial and Target
c_initial_linear = jnp.linspace(0.85, 1.0, n)
ctarget_linear = jnp.linspace(0.9, 1.0, n)
# Run Adam optimization
print("Starting Adam optimization...")
result_adam = optax_adam_linear(c_initial_linear, 1000)
# Run L-BFGS optimization
print("\nStarting L-BFGS optimization...")
result_lbfgs = tfp_lbfgs_linear(c_initial_linear)
# Compare results
adam_rmse = jnp.sqrt(jnp.mean((result_adam - ctarget_linear)**2))
lbfgs_rmse = jnp.sqrt(jnp.mean((result_lbfgs - ctarget_linear)**2))
print(f"\nFinal Results:")
print(f"Adam RMSE: {adam_rmse:.8f}")
print(f"L-BFGS RMSE: {lbfgs_rmse:.8f}")
print(f"L-BFGS improvement: {adam_rmse/lbfgs_rmse:.1f}x better")
Starting Adam optimization... Iteration 0: Loss = 3.807940, Velocity RMSE = 0.028013 Iteration 200: Loss = 0.008648, Velocity RMSE = 0.015287 Iteration 400: Loss = 0.021045, Velocity RMSE = 0.016096 Iteration 600: Loss = 0.014158, Velocity RMSE = 0.016653 Iteration 800: Loss = 0.029612, Velocity RMSE = 0.016825 Starting L-BFGS optimization... Final Results: Adam RMSE: 0.01696190 L-BFGS RMSE: 0.01419833 L-BFGS improvement: 1.2x better
In [13]:
Copied!
# Define loss function for linear velocity profile
@jit
def compute_loss_linear(c_array):
"""Loss function for spatially-varying velocity model"""
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_linear)
# Gradient function
grad_loss_linear = jit(grad(compute_loss_linear))
# Test initial loss and gradient
initial_loss_linear = compute_loss_linear(c_initial_linear)
initial_grad_linear = grad_loss_linear(c_initial_linear)
print(f"Initial loss: {initial_loss_linear:.6f}")
print(f"Gradient shape: {initial_grad_linear.shape}")
print(f"Gradient norm: {jnp.linalg.norm(initial_grad_linear):.6f}")
# Define loss function for linear velocity profile
@jit
def compute_loss_linear(c_array):
"""Loss function for spatially-varying velocity model"""
u2 = wave_propagation(c_array)
return jnp.linalg.norm(u2 - target_linear)
# Gradient function
grad_loss_linear = jit(grad(compute_loss_linear))
# Test initial loss and gradient
initial_loss_linear = compute_loss_linear(c_initial_linear)
initial_grad_linear = grad_loss_linear(c_initial_linear)
print(f"Initial loss: {initial_loss_linear:.6f}")
print(f"Gradient shape: {initial_grad_linear.shape}")
print(f"Gradient norm: {jnp.linalg.norm(initial_grad_linear):.6f}")
Initial loss: 3.944904 Gradient shape: (1000,) Gradient norm: 4.976274
In [14]:
Copied!
# Optimizers for linear profile
def optax_adam_linear(params, niter):
"""Optimize spatially-varying velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
opt_state = optimizer.init(params)
for i in range(niter):
grads = grad_loss_linear(params)
updates, opt_state = optimizer.update(grads, opt_state)
params = optax.apply_updates(params, updates)
if i % 200 == 0:
loss_val = compute_loss_linear(params)
velocity_rmse = jnp.sqrt(jnp.mean((params - ctarget_linear)**2))
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity RMSE = {velocity_rmse:.6f}")
return params
def tfp_lbfgs_linear(params):
"""Optimize using L-BFGS"""
# For TFP L-BFGS, we need a function that returns both value and gradients
from jax import value_and_grad
value_and_grad_fn = jit(value_and_grad(compute_loss_linear))
results = tfp.optimizer.lbfgs_minimize(
value_and_grad_fn,
initial_position=params,
tolerance=1e-5
)
return results.position
# Run Adam optimization
print("Starting Adam optimization...")
result_adam = optax_adam_linear(c_initial_linear, 1000)
# Run L-BFGS optimization
print("\nStarting L-BFGS optimization...")
result_lbfgs = tfp_lbfgs_linear(c_initial_linear)
# Compare results
adam_rmse = jnp.sqrt(jnp.mean((result_adam - ctarget_linear)**2))
lbfgs_rmse = jnp.sqrt(jnp.mean((result_lbfgs - ctarget_linear)**2))
print(f"\nFinal Results:")
print(f"Adam RMSE: {adam_rmse:.8f}")
print(f"L-BFGS RMSE: {lbfgs_rmse:.8f}")
print(f"L-BFGS improvement: {adam_rmse/lbfgs_rmse:.1f}x better")
# Optimizers for linear profile
def optax_adam_linear(params, niter):
"""Optimize spatially-varying velocity using Adam optimizer"""
start_learning_rate = 1e-3
optimizer = optax.adam(start_learning_rate)
opt_state = optimizer.init(params)
for i in range(niter):
grads = grad_loss_linear(params)
updates, opt_state = optimizer.update(grads, opt_state)
params = optax.apply_updates(params, updates)
if i % 200 == 0:
loss_val = compute_loss_linear(params)
velocity_rmse = jnp.sqrt(jnp.mean((params - ctarget_linear)**2))
print(f"Iteration {i:4d}: Loss = {loss_val:.6f}, Velocity RMSE = {velocity_rmse:.6f}")
return params
def tfp_lbfgs_linear(params):
"""Optimize using L-BFGS"""
# For TFP L-BFGS, we need a function that returns both value and gradients
from jax import value_and_grad
value_and_grad_fn = jit(value_and_grad(compute_loss_linear))
results = tfp.optimizer.lbfgs_minimize(
value_and_grad_fn,
initial_position=params,
tolerance=1e-5
)
return results.position
# Run Adam optimization
print("Starting Adam optimization...")
result_adam = optax_adam_linear(c_initial_linear, 1000)
# Run L-BFGS optimization
print("\nStarting L-BFGS optimization...")
result_lbfgs = tfp_lbfgs_linear(c_initial_linear)
# Compare results
adam_rmse = jnp.sqrt(jnp.mean((result_adam - ctarget_linear)**2))
lbfgs_rmse = jnp.sqrt(jnp.mean((result_lbfgs - ctarget_linear)**2))
print(f"\nFinal Results:")
print(f"Adam RMSE: {adam_rmse:.8f}")
print(f"L-BFGS RMSE: {lbfgs_rmse:.8f}")
print(f"L-BFGS improvement: {adam_rmse/lbfgs_rmse:.1f}x better")
Starting Adam optimization... Iteration 0: Loss = 3.807940, Velocity RMSE = 0.028013 Iteration 200: Loss = 0.008648, Velocity RMSE = 0.015287 Iteration 400: Loss = 0.021045, Velocity RMSE = 0.016096 Iteration 600: Loss = 0.014158, Velocity RMSE = 0.016653 Iteration 800: Loss = 0.029612, Velocity RMSE = 0.016825 Starting L-BFGS optimization... Final Results: Adam RMSE: 0.01696190 L-BFGS RMSE: 0.01419833 L-BFGS improvement: 1.2x better
In [15]:
Copied!
# Visualize linear velocity optimization results
wave_adam = wave_propagation(result_adam)
wave_lbfgs = wave_propagation(result_lbfgs)
wave_initial = wave_propagation(c_initial_linear)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Velocity model comparison
axes[0, 0].plot(x0, ctarget_linear, 'k-', linewidth=3, label='Target velocity', alpha=0.8)
axes[0, 0].plot(x0, c_initial_linear, 'gray', linestyle=':', linewidth=2, label='Initial guess')
axes[0, 0].plot(x0, result_adam, 'b-', linewidth=2, label='Adam result')
axes[0, 0].plot(x0, result_lbfgs, 'r--', linewidth=2, label='L-BFGS result')
axes[0, 0].set_xlabel('Position')
axes[0, 0].set_ylabel('Velocity')
axes[0, 0].set_title('Velocity Model Recovery')
axes[0, 0].legend()
axes[0, 0].grid(True)
# Wavefield comparison
axes[0, 1].plot(x0, target_linear, 'k-', linewidth=3, label='Target', alpha=0.8)
axes[0, 1].plot(x0, wave_initial, 'gray', linestyle=':', linewidth=2, label='Initial')
axes[0, 1].plot(x0, wave_adam, 'b-', linewidth=2, label='Adam prediction')
axes[0, 1].plot(x0, wave_lbfgs, 'r--', linewidth=2, label='L-BFGS prediction')
axes[0, 1].set_xlabel('Position')
axes[0, 1].set_ylabel('Amplitude')
axes[0, 1].set_title('Wavefield Predictions')
axes[0, 1].legend()
axes[0, 1].grid(True)
# Error comparison
adam_error = jnp.abs(result_adam - ctarget_linear)
lbfgs_error = jnp.abs(result_lbfgs - ctarget_linear)
axes[1, 0].plot(x0, adam_error, 'b-', linewidth=2, label=f'Adam (RMSE: {adam_rmse:.6f})')
axes[1, 0].plot(x0, lbfgs_error, 'r--', linewidth=2, label=f'L-BFGS (RMSE: {lbfgs_rmse:.6f})')
axes[1, 0].set_xlabel('Position')
axes[1, 0].set_ylabel('|Error|')
axes[1, 0].set_title('Velocity Estimation Errors')
axes[1, 0].legend()
axes[1, 0].grid(True)
# Summary statistics
summary_text = f'''Algorithm Comparison:
Adam Optimizer:
• RMSE: {adam_rmse:.8f}
• Max error: {jnp.max(adam_error):.8f}
• Mean error: {jnp.mean(adam_error):.8f}
L-BFGS Optimizer:
• RMSE: {lbfgs_rmse:.8f}
• Max error: {jnp.max(lbfgs_error):.8f}
• Mean error: {jnp.mean(lbfgs_error):.8f}
L-BFGS is {adam_rmse/lbfgs_rmse:.1f}× more accurate'''
axes[1, 1].text(0.05, 0.95, summary_text, transform=axes[1, 1].transAxes,
fontsize=10, ha='left', va='top',
bbox=dict(boxstyle='round', facecolor='lightblue', alpha=0.8))
axes[1, 1].set_title('Optimization Comparison')
axes[1, 1].axis('off')
plt.tight_layout()
plt.show()
# Visualize linear velocity optimization results
wave_adam = wave_propagation(result_adam)
wave_lbfgs = wave_propagation(result_lbfgs)
wave_initial = wave_propagation(c_initial_linear)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Velocity model comparison
axes[0, 0].plot(x0, ctarget_linear, 'k-', linewidth=3, label='Target velocity', alpha=0.8)
axes[0, 0].plot(x0, c_initial_linear, 'gray', linestyle=':', linewidth=2, label='Initial guess')
axes[0, 0].plot(x0, result_adam, 'b-', linewidth=2, label='Adam result')
axes[0, 0].plot(x0, result_lbfgs, 'r--', linewidth=2, label='L-BFGS result')
axes[0, 0].set_xlabel('Position')
axes[0, 0].set_ylabel('Velocity')
axes[0, 0].set_title('Velocity Model Recovery')
axes[0, 0].legend()
axes[0, 0].grid(True)
# Wavefield comparison
axes[0, 1].plot(x0, target_linear, 'k-', linewidth=3, label='Target', alpha=0.8)
axes[0, 1].plot(x0, wave_initial, 'gray', linestyle=':', linewidth=2, label='Initial')
axes[0, 1].plot(x0, wave_adam, 'b-', linewidth=2, label='Adam prediction')
axes[0, 1].plot(x0, wave_lbfgs, 'r--', linewidth=2, label='L-BFGS prediction')
axes[0, 1].set_xlabel('Position')
axes[0, 1].set_ylabel('Amplitude')
axes[0, 1].set_title('Wavefield Predictions')
axes[0, 1].legend()
axes[0, 1].grid(True)
# Error comparison
adam_error = jnp.abs(result_adam - ctarget_linear)
lbfgs_error = jnp.abs(result_lbfgs - ctarget_linear)
axes[1, 0].plot(x0, adam_error, 'b-', linewidth=2, label=f'Adam (RMSE: {adam_rmse:.6f})')
axes[1, 0].plot(x0, lbfgs_error, 'r--', linewidth=2, label=f'L-BFGS (RMSE: {lbfgs_rmse:.6f})')
axes[1, 0].set_xlabel('Position')
axes[1, 0].set_ylabel('|Error|')
axes[1, 0].set_title('Velocity Estimation Errors')
axes[1, 0].legend()
axes[1, 0].grid(True)
# Summary statistics
summary_text = f'''Algorithm Comparison:
Adam Optimizer:
• RMSE: {adam_rmse:.8f}
• Max error: {jnp.max(adam_error):.8f}
• Mean error: {jnp.mean(adam_error):.8f}
L-BFGS Optimizer:
• RMSE: {lbfgs_rmse:.8f}
• Max error: {jnp.max(lbfgs_error):.8f}
• Mean error: {jnp.mean(lbfgs_error):.8f}
L-BFGS is {adam_rmse/lbfgs_rmse:.1f}× more accurate'''
axes[1, 1].text(0.05, 0.95, summary_text, transform=axes[1, 1].transAxes,
fontsize=10, ha='left', va='top',
bbox=dict(boxstyle='round', facecolor='lightblue', alpha=0.8))
axes[1, 1].set_title('Optimization Comparison')
axes[1, 1].axis('off')
plt.tight_layout()
plt.show()
Advanced Optimization: Newton's Method and BFGS¶
Newton's Method for Optimization¶
Newton's method finds minima by using second-order information: $$x_{k+1} = x_k - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k)$$
Where:
- $x_k$ is the current estimate
- $\nabla^2 f(x_k)$ is the Hessian matrix (second derivatives)
- $\nabla f(x_k)$ is the gradient vector
Challenge: Computing and inverting the Hessian is expensive for large problems.
BFGS (Broyden-Fletcher-Goldfarb-Shanno)¶
BFGS approximates the inverse Hessian iteratively: $$H_{k+1} = (I - \rho_k s_k y_k^T) H_k (I - \rho_k y_k s_k^T) + \rho_k s_k s_k^T$$
Where:
- $s_k = x_{k+1} - x_k$ (step difference)
- $y_k = \nabla f(x_{k+1}) - \nabla f(x_k)$ (gradient difference)
- $\rho_k = \frac{1}{y_k^T s_k}$
L-BFGS (Limited-memory BFGS) stores only recent history, making it suitable for large problems.
Adam vs L-BFGS Comparison¶
| Aspect | Adam | L-BFGS |
|---|---|---|
| Type | First-order (gradients only) | Quasi-Newton (approximate second-order) |
| Memory | O(1) per parameter | O(m) history vectors |
| Convergence | Robust, good for noisy functions | Superlinear for smooth functions |
| Best for | Large-scale, noisy problems | Smooth, deterministic functions |
Our Results: L-BFGS achieved significantly better accuracy for the smooth wave equation optimization, demonstrating the power of second-order methods for well-conditioned problems.
The Power of Differentiable Simulation¶
What we've demonstrated:
- Physics-Based Model: Realistic wave equation solver with finite differences
- Automatic Differentiation: JAX computed exact gradients through entire simulation
- Scalable Optimization: From 1 parameter (constant) to 1000 parameters (linear profile)
- Algorithm Comparison: Adam vs L-BFGS trade-offs in practice
Key Results:
- Constant velocity: Perfect recovery with gradient descent
- Linear profile: High-fidelity reconstruction of spatially-varying parameters
- L-BFGS advantage: Superior convergence for smooth optimization landscapes
The Revolution: Physics simulations are now learnable components that can be optimized end-to-end with gradient descent, enabling inverse problems that were previously intractable.
Applications¶
Geophysics: Subsurface imaging, earthquake location, Earth structure Medical imaging: Ultrasound tomography, photoacoustic imaging Materials science: Non-destructive testing, property characterization Engineering: Structural health monitoring, design optimization
Next Steps¶
- Explore the interactive projectile demo:
projectile.md - Try different velocity models (step functions, Gaussian anomalies)
- Experiment with other PDEs (heat, elasticity, Maxwell)
- Implement multi-objective optimization with regularization
The Future: Differentiable simulation bridges physics and machine learning, enabling scientific discovery through optimization.